Задача 78458 Дано уравнение параболы y^2+6y+2x-1=0....
Условие
Решение
(y - y0)^2 = 2p(x - x0)
Нам нужно привести уравнение к такому виду.
y^2 + 6y + 2x - 1 = 0
y^2 + 6y + 9 - 9 + 2x - 1 = 0
(y + 3)^2 + 2x - 10 = 0
(y + 3)^2 = -2x + 10
[b](y + 3)^2 = 2(-x + 5)[/b]
Вершина параболы находится в точке (5; -3).
Коэффициент [b]p = -1[/b]
Так как p < 0, то ветви параболы направлены влево.
Уравнение оси параболы:
[b]y = -3[/b]
Координаты фокуса параболы: F(5 + 1/2*p; -3) = (5 - 0,5; -3)
[b]F(4,5; -3)[/b]
Уравнение директрисы: x - x0 = -p/2.
x - 5 = 1/2
[b]x = 5,5[/b]
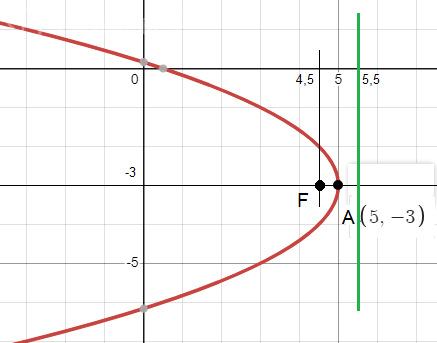
График приведен на рисунке.
Ось показана черным цветом.
Директриса показана зелёным цветом.