Задача 78433 ——— R EQFVT*;;%—; ОННЕ Е нении ен Ы — НЕ...
Условие

Решение
Уравнения сторон:
7*x + 4*y = -67
-8*x + 8*y + 24 = 0
Если подставить точку А в эти уравнения, то получится:
7*7 + 4*(-7) = 49 - 28 = 21 ≠ -67
-8*7 + 8*(-7) + 24 = -56 - 56 + 24 = -88 ≠ 0
Это значит, что точка А не принадлежит ни одной из этих прямых.
Значит, точка А есть точка пересечения двух сторон, которые параллельны этим.
Найдем координаты точки С пересечения этих сторон.
{ 7*x + 4*y + 67 = 0
{ -8*x + 8*y + 24 = 0
Умножаем 1 уравнение на -2:
{ -14*x - 8*y - 134 = 0
{ -8*x + 8*y + 24 = 0
Складываем уравнения:
-22x + 0y - 110 = 0
-22x = 110
x = 110/(-22) = -5
Подставляем в уравнение:
7*(-5) + 4*y + 67 = 0
4*y = -67 + 35 = -32
y = -32/4 = -8
[b]C(-5; -8)[/b]
Теперь проведем две прямые, параллельные данным, через точку А:
1) 7*(x - 7) + 4*(y + 7) = 0
7*x - 49 + 4*y + 28 = 0
7*x + 4*y - 21 = 0
2) -8*(x - 7) + 8*(y + 7) = 0
-8*x + 56 + 8*y + 56 = 0
-8*x + 8*y + 112 = 0
А теперь найдем точки B и D, которые являются точками пересечения этих новых прямых с заданными прямыми:
1)
{ 7*x + 4*y - 21 = 0
{ -8*x + 8*y + 24 = 0
Умножаем 1 уравнение на -2:
{ -14*x - 8*y + 42 = 0
{ -8*x + 8*y + 24 = 0
Складываем уравнения:
-22x + 0y + 66 = 0
x = -66/(-22) = 3
Подставляем в уравнение:
7*3 + 4*y - 21 = 0
21 + 4y - 21 = 0
y = 0
[b]B(3; 0)[/b]
2)
{ 7*x + 4*y + 67 = 0
{ -8*x + 8*y + 112 = 0
Умножаем 1 уравнение на -2:
{ -14*x - 8*y - 134 = 0
{ -8*x + 8*y + 112 = 0
Складываем уравнения:
-22x + 0y - 22 = 0
x = 22/(-22) = -1
Подставляем в уравнение:
-8*(-1) + 8y + 112 = 0
8 + 8y + 112 = 0
8y = -120
y = -120/8 = -15
[b]D(-1; -15)[/b]
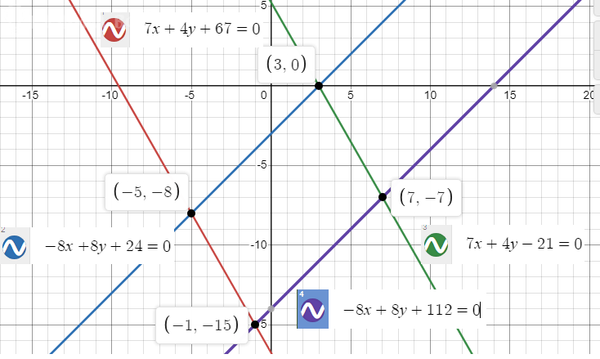
Ответ: A(7; -7); B(3; 0); C(-5; -8); D(-1; -15)
Всё это показано на рисунке