Задача 78398 логическое выражение, которое принимает...

Mip

8 октября 2024 г. в 07:08

логическое выражение, которое принимает значение "TRUE" тогда и только тогда, когда точка с координатами (x, y) принадлежит заштрихованной области и FALSE в противном случае.Помогите определить границы заштрихованной области,пожалуйста.

Удачник66

8 октября 2024 г. в 08:18

★

Точки пересечения параболы и прямой:
x² = 2 – x
x² + x – 2 = 0
(x – 1)(x + 2) = 0
x1 = –2; x2 = 1
y(–2) = (–2)² = 4; y(–2) = 2 – (–2) = 4
y(1) = 1² = 1; y(1) = 2 – 1 = 1

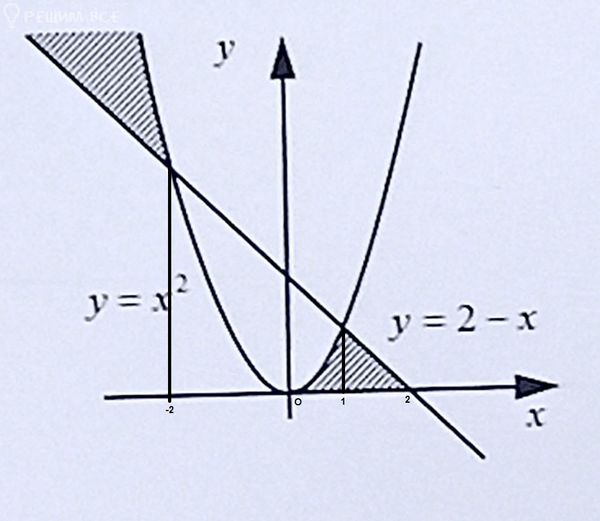
Точки пересечения: (–2; 4); (1; 1)
В левой области x ∈ (–oo; –2]; 2 – x ≤ y ≤ x²
В правой области две части.
1) y ≥ 0, x ∈ [0; 1], y(0) = 0² = 0; y(1) = 1² = 1
2) y ≥ 0, x ∈ [1; 2]; y(1) = 2 – 1 = 1; y(2) = 2 – 2 = 0

Границы заштрихованной области:
1) x ∈ (–oo; –2]
y ∈ [2 – x; x²]

2) x ∈ [0; 1]
y ∈ [0; x²]

3) x ∈ [1; 2]
y ∈ [0; 2 – x]

На графике я показал все области.