Задача 78384 Дробно-линейная функция задана...

6700b943bc8c5879e2b80355

10/5/2024 3:59:51 AM

Дробно-линейная функция задана уравнением: ()=(ax+3)/(2x+d).Асимптоты функции имеют уравнения х=2,5, у 1,5. Найдите значение переменных.
б) Используя результаты предыдущего действия: i)приведите функцию f(x)=ax+3/2x+b к виду у=n+k/x+m;
ii) найдите точки пересечения функции с осями координат;

626fab9a354ab65fb2f43abb

10/12/2024 9:09:31 AM

★

Ну вот, теперь все понятно!
[b]3. [/b]Функция: [m]f(x) = \frac{ax+3}{2x+d}[/m]
Асимптоты: x = 2,5; y = 1,5
Привести функцию к виду: [m]y = n + \frac{k}{x+m}[/m]
Решение.
Если вертикальная асимптота x = 2,5, то в знаменателе должно быть:
x - 2,5 = 0,5*(2x - 5)
То есть в знаменателе (2x - 5), коэффициент 0,5 здесь не важен.
[b]d = -5[/b]
Если горизонтальная асимптота y = 1,5, то должно быть:
[m]\frac{ax}{2x} = \frac{a}{2} = 1,5 = \frac{3}{2}[/m]
[b]a = 3[/b]
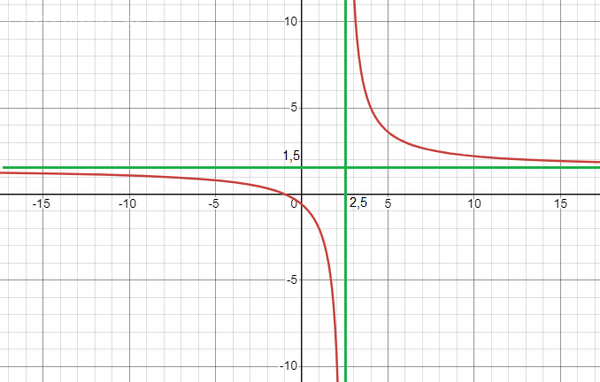
Функция: [m]f(x) = \frac{3x+3}{2x-5}[/m]
График этой функции на рисунке. Асимптоты показаны зелёными линиями.

Приводим функцию к виду: [m]y = n + \frac{k}{x+m}[/m]
[m]y = \frac{3x+3}{2x-5} = \frac{3/2*(2x-5)+5 \cdot 3/2 +3}{2x-5} = \frac{3}{2} + \frac{15/2+3}{2x-5} = \frac{3}{2} + \frac{21/2}{2x-5} [/m]
[m]y = \frac{3}{2} + \frac{21/4}{x-5/2}[/m]
[b]n = 3/2; k = 21/4; m = -5/2[/b]

[b]4.[/b] Построить обратную функцию к полученной функции
[m]y = \frac{3x+3}{2x-5}[/m]
Построить обратную функцию - это значит выразить x через y.
Выразим функцию, как нам было задано, в виде:
[m]y = \frac{3}{2} + \frac{21/4}{x-5/2}[/m]
[m]y - \frac{3}{2} = \frac{21/4}{x-5/2}[/m]
[m]x - \frac{5}{2} = \frac{21/4}{y - 3/2}[/m]
[m]x = \frac{5}{2} + \frac{21/4}{y - 3/2} = \frac{5(y-3/2) + 2 \cdot 21/4}{2(y-3/2)} = \frac{5y-15/2 + 21/2}{2y-3}[/m]
[m]x = \frac{5y + 3}{2y-3}[/m]