Задача 78381 Обоснуйте формулы сведения, используя...
Условие
Решение
Во-первых, у вас раздел написан: Химия, а вопрос по математике.
Во-вторых, не "формулы сведения", а "формулы приведения".
Запишем сначала сами формулы:
sin (-a) = -sin a; cos (-a) = cos a
sin (π/2 - a) = cos a; cos (π/2 - a) = sin a
sin (π/2 + a) = cos a; cos (π/2 + a) = -sin a
sin (π - a) = sin a; cos (π - a) = -cos a
sin (π + a) = -sin a; cos (π + a) = -cos a
sin (3π/2 - a) = -cos a; cos (3π/2 - a) = -sin a
sin (3π/2 + a) = -cos a; cos (3π/2 + a) = sin a
sin (2π - a) = sin (-a) = -sin a; cos (2π - a) = cos (-a) = cos a
sin (2π + a) = sin a; cos (2π + a) = cos a
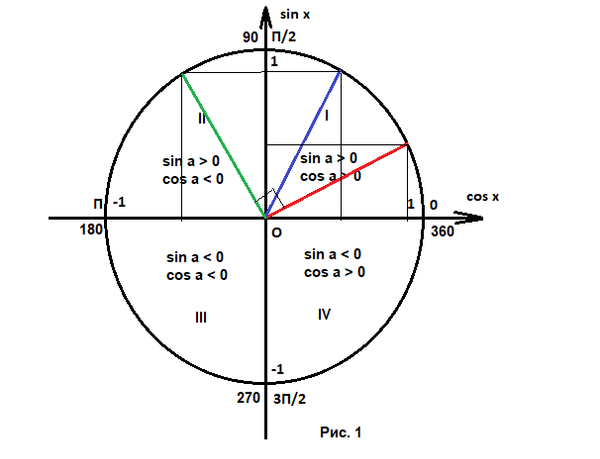
Покажем всё это на тригонометрическом круге.
На Рис. 1 красным показан угол а, синим угол π/2 - a, зеленым угол π/2 + a.
Угол между красным и зеленым отрезками - прямой, это показано квадратиком.
Как видим, у угла π/2 - a по сравнению с углом а sin и cos поменялись местами.
sin (π/2 - x) = cos x; cos (π/2 - x) = sin x
А у угла π/2 + a синус такой же, как у π/2 - a, а косинус противоположный.
sin (π/2 + x) = cos x; cos (π/2 + x) = -sin x
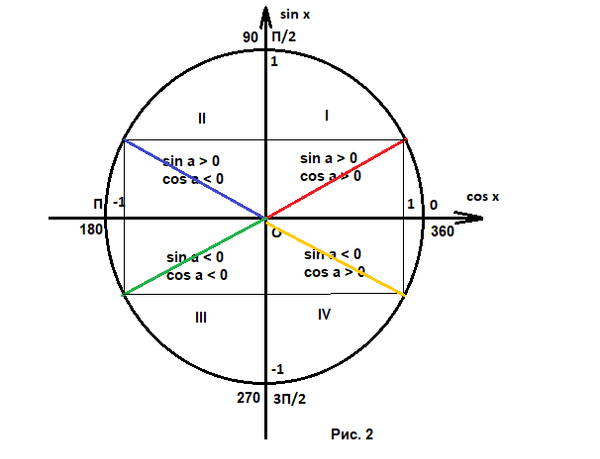
На Рис. 2 красным изображен угол а, оранжевым угол -а.
Как видим, cos (-a) остался прежним, а sin (-a) противоположен sin a.
sin (-a) = -sin a; cos (-a) = cos a
Синим показан угол π - a, зеленым - угол π + a.
У угла π - a синус такой же, как у угла а, а косинус противоположный.
sin (π - a) = sin a; cos (π - a) = -cos a
У угла π + a и синус и косинус противоположны синусу и косинусу угла а.
sin (π + a) = -sin a; cos (π + a) = -cos a
С углами 3π/2 - a и 3π/2 + a я вам предлагаю разобраться самостоятельно.
Они такие же, как π/2 - a и π/2 + a, синусы и косинусы меняются местами.
С углами 2π - a и 2π + a всё ясно сразу.
2π - это период синуса и косинуса, поэтому углы 2π - a = -а, 2π + a = а.
И все функции тоже будут повторяться.