Задача 78380 В треугольнике со сторонами 6 см, 10 см,...

67028ae6bc8c5879e2b80422

10/6/2024 1:05:48 PM

В треугольнике со сторонами 6 см, 10 см, 8 см проведены две медианы BN и AM (O – точка их пересечения). Найти площадь фигуры NOMC.

626fab9a354ab65fb2f43abb

10/6/2024 3:14:20 PM

★

Смотрите рисунок.
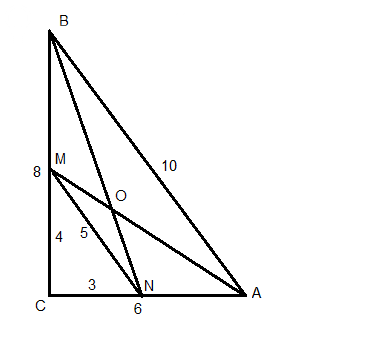
Треугольник со сторонами 6 см, 8 см, 10 см - прямоугольный.
CN = AC/2 = 6/2 = 3 см
CM = BC/2 = 8/2 = 4 см
MN = AB/2 = 10/2 = 5 см
Длины медиан можно найти из формулы:
[m]m_{a} = \frac{1}{2} \sqrt{2b^2 + 2c^2 - a^2}[/m]
[m]|BN| = \frac{1}{2} \sqrt{2|BC|^2 + 2|AB|^2 - |AC|^2} = \frac{1}{2} \sqrt{2 \cdot 8^2 + 2 \cdot 10^2 - 6^2} =[/m]
[m]= \frac{1}{2} \sqrt{128 + 200 - 36} = \frac{1}{2} \sqrt{292} = \frac{1}{2} \sqrt{4 \cdot 73} = \sqrt{73}[/m]
[m]|AM| = \frac{1}{2} \sqrt{2|AC|^2 + 2|AB|^2 - |BC|^2} = \frac{1}{2} \sqrt{2 \cdot 6^2 + 2 \cdot 10^2 - 8^2} =[/m]
[m]= \frac{1}{2} \sqrt{72 + 200 - 64} = \frac{1}{2} \sqrt{208} = \frac{1}{2} \sqrt{4 \cdot 52} = \sqrt{52}[/m]
Как известно, точка пересечения медиан делит их в отношении 2:1 от вершин.
Значит:
[m]|ON| = \frac{1}{3} |BN| = \frac{\sqrt{73}}{3}[/m]
[m]|OM| = \frac{1}{3} |AM| = \frac{\sqrt{52}}{3}[/m]
Площадь фигуры NOMC складывается из площадей треугольников MNC и MNO.
Площадь прямоугольного треугольника MNC найти легко:
[m]S(MNC) = \frac{|MC| \cdot |NC|}{2} = \frac{4 \cdot 3}{2} = 6[/m] см^2
Чтобы найти площадь треугольника MNO, сначала найдем угол MON через теорему косинусов:
[m]|MN|^2 = |ON|^2 + |OM|^2 - 2|ON| \cdot |OM| \cdot \cos MON[/m]
[m]5^2 = \frac{73}{9} + \frac{52}{9} - 2 \cdot \frac{\sqrt{73}}{3} \cdot \frac{\sqrt{52}}{3} \cdot \cos MON[/m]
[m]25 = \frac{125}{9} - \frac{2\sqrt{73 \cdot 52}}{9} \cdot \cos MON = \frac{125}{9} - \frac{4\sqrt{73 \cdot 13}}{9} \cdot \cos MON[/m]
[m]\frac{4\sqrt{949}}{9} \cdot \cos MON = \frac{125}{9} - \frac{225}{9} = -\frac{100}{9}[/m]
[m]\cos MON = -\frac{100}{4\sqrt{949}} = -\frac{25}{\sqrt{949}}[/m]
[m]\sin MON = \sqrt{1 - \cos^2 MON} = \sqrt{1 - \frac{25^2}{949}} = \sqrt{\frac{949-625}{949}} = \sqrt{\frac{324}{949}} = \frac{18}{\sqrt{949}}[/m]
Площадь треугольника MNO находим по формуле с синусом:
[m]S(MNO) = \frac{1}{2} \cdot |ON| \cdot |OM| \cdot \sin MON = \frac{1}{2} \cdot \frac{\sqrt{73}}{3} \cdot \frac{\sqrt{52}}{3} \cdot \frac{18}{\sqrt{949}} =[/m]
[m]= \frac{\sqrt{73} \cdot 2 \sqrt{13} \cdot 18}{2 \cdot 9 \cdot \sqrt{73 \cdot 13}} = \frac{2 \cdot 18}{2 \cdot 9 } = 2[/m] см^2
Площадь всей фигуры NOMC:
[m]S(NOMC) = S(MNC) + S(MNO) = 6 + 2 = 8[/m] см^2

Ответ: 8 см^2