Задача 78356 ...
Условие
Дано: 1à| = 2, 16| = 1, 4 = (à,b) = 3. Найти модуль вектора E= 28- 36.
математика ВУЗ
475
Решение
★
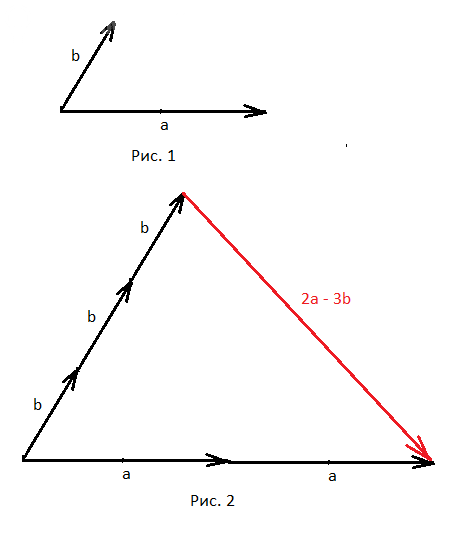
На Рис. 1 изображены вектора а и b, |a| = 2; |b| = 1; угол (a; b) = π/3
На Рис. 2 изображены вектора 2а и 3b и красным вектор 2a - 3b.
|2a| = 2*2 = 4; |3b| = 3*1 = 3
φ = (2a; 3b) = (a; b) = π/3
По теореме косинусов:
|2a - 3b|^2 = |2a|^2 + |3b|^2 - 2*|2a|*|3b|*cos φ
|2a - 3b|^2 = 4^2 + 3^2 - 2*4*3*1/2 = 16 + 9 - 12 = 13
|2a - 3b| = sqrt(13)