Задача 7834 Основания равнобедренной трапеции равны...

Julia_Trusova

16 марта 2016 г.

Основания равнобедренной трапеции равны 8 и 2, а боковое ребро равно 5. Найдите расстояние между центрами вписанной и описанной окружностей.

BC=2, AD=8, AB=CD=5 – по условию
О–центр вписанной окружности, О1–центр описанной окружности.
Пусть радиус вписанной окружности – r, радиус описанной окружности – R.
СН–высота трапеции,
СН=2·r
HD=(AD–BC)/2=(8–2)/2=3
Из △СНD по теореме Пифагора:
CH=√5²–3²=√25–9=√16=4
⇒r=CH/2=4/2=2
OE=r=2
Найдем R из △ACD:
R=(AC·CD·AD)/(4·S(ACD))
Из △АСН:
АН=AD–HD=8–3=5
По теореме Пифагора:
АС=√4²+5²=√16+25=√41
S(ACD)=1/2·AD·CH=1/2·8·4=16
R=(√41·5·8)/(4·16)=(40·√41)/64=(5·√41)/8
Из △О1ЕD:
ED=1/2·AD=1/2·8=4
По теореме Пифагора:
О1Е=√((5·√41)/8)²–4²=√(25·41)/64–16=√(25·41–16·64)/64=1/8·1=1/8
OO1=OE–O1E=2–1/8=15/8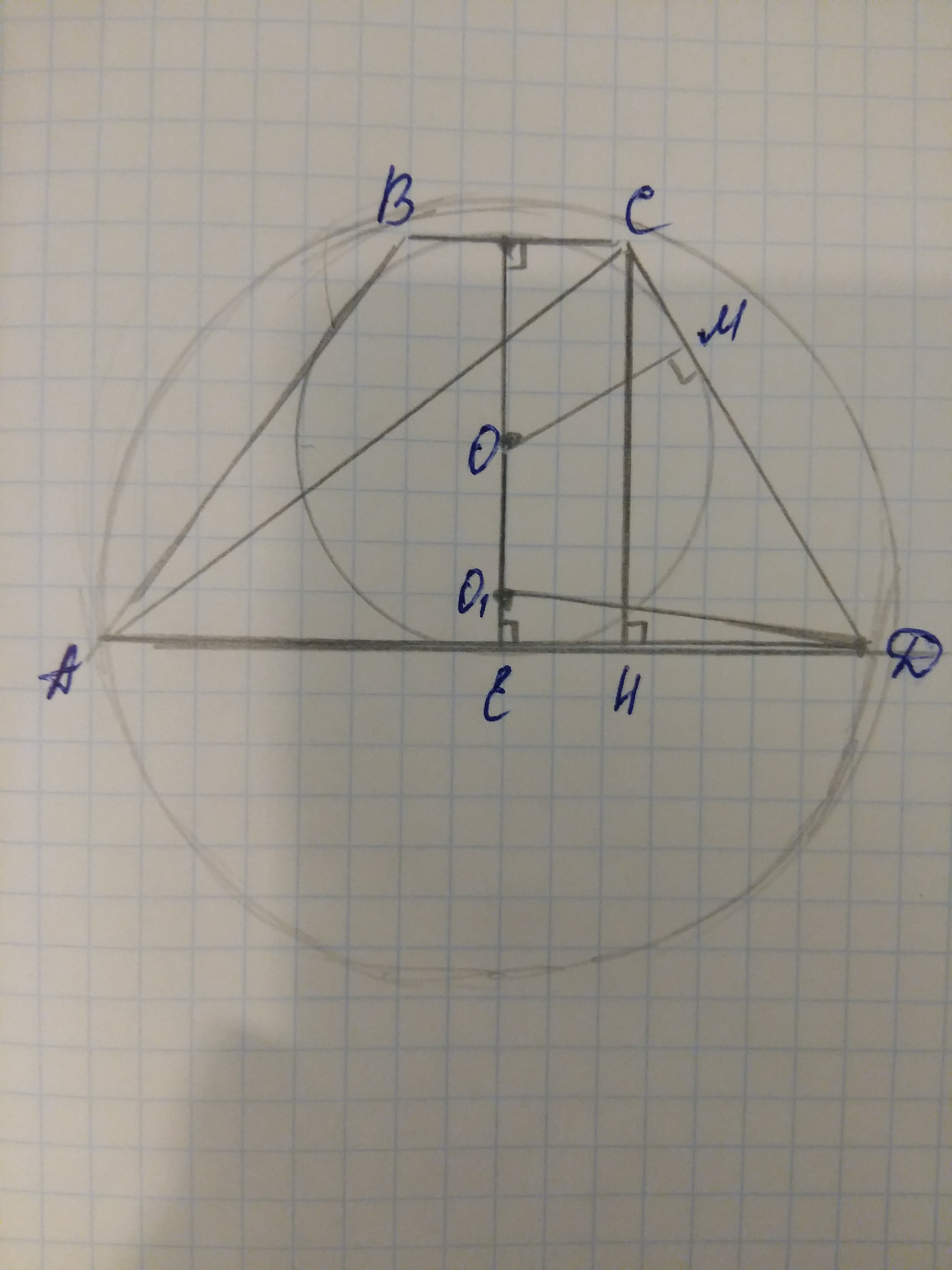

Ответ: 15/8