Задача 78338 Дан треугольник MNK, в котором MN = NK,...
Условие
Решение
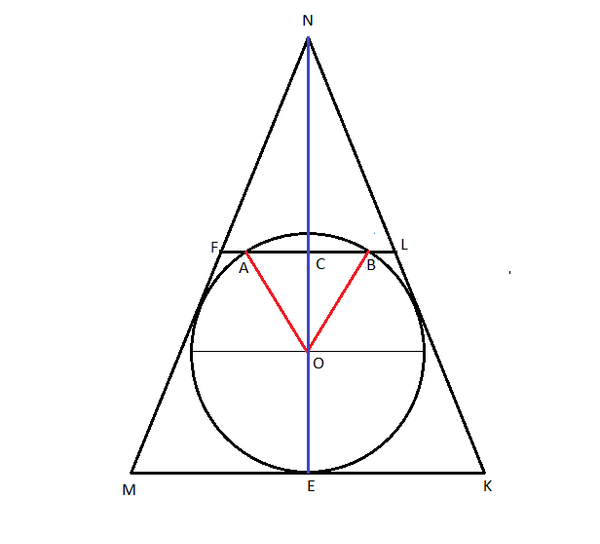
Дано: MN = NK, MK = 26, AB = 5,
FL - средняя линия треугольника MNK,
Найти: наибольшую длину MN
Решение.
FL = MK/2 = 26/2 = 13
FC = CL = FL/2 = 13/2 = 6,5
ME = EK = MK/2 = 26/2 = 13
FA = BE = (FL - AB)/2 = (13 - 5)/2 = 4
AC = CB = AB/2 = 5/2 = 2,5
Обозначим:
MN = NK = b
OA = OB = OE = r
NE = H
MF = FN = MN/2 = b/2
NC = CE = H/2
По теореме Пифагора для треугольника MNE:
MN^2 = ME^2 + NE^2
b^2 = 13^2 + H^2
b^2 = H^2 + 169 (1)
По теореме Пифагора для треугольника ACO:
OC^2 = OA^2 - AC^2 = r^2 - 2,5^2
Но с другой стороны:
OC = CE - OE = H/2 - r
Получаем уравнение:
r^2 - 2,5^2 = (H/2 - r)^2
r^2 - 6,25 = H^2/4 - H*r + r^2
H*r = H^2/4 + 25/4
r = (H^2 + 25)/(4H) (2)
По известным формулам площади треугольника:
S = a*H/2 = p*r = P*r/2
где P = a + 2b = 26 + 2b - периметр треугольника MNK
Отсюда:
26*H = (26 + 2b)*r
Разделим всё на 2 и выразим r:
r = 13H/(13 + b) (3)
Получаем новое уравнение из (2) и (3):
[m]\frac{H^2 + 25}{4H} = \frac{13H}{13 + b}[/m]
[m]13 + b = \frac{4H \cdot 13H}{H^2 + 25} = \frac{52H^2}{H^2 + 25}[/m]
[m]b = \frac{52H^2}{H^2 + 25} - 13 = \frac{52H^2 - 13H^2 - 25 \cdot 13}{H^2 + 25} [/m]
[m]b = \frac{39H^2- 325}{H^2 + 25} = \frac{39(H^2+25)-39 \cdot 25 -325}{H^2 + 25}[/m]
[m]b = 39 - \frac{1300}{H^2 + 25}[/m]
Но из (1):
b^2 = H^2 + 169
Приравниваем:
[m]H^2 + 169 = (39 - \frac{1300}{H^2 + 25})^2[/m]
Это сложное уравнение, которое приводится к уравнению 4 степени.
Оно имеет 2 действительных корня. Онлайн калькуляторы показывают:
H1 = sqrt(27); H2 = sqrt(1275)
Естественно, чем больше будет высота H, тем больше боковая b = MN.
H = sqrt(1275)
[m]b = 39 - \frac{1300}{H^2 + 25} = 39 - \frac{1300}{1275 + 25} = 39 - \frac{1300}{1300} = 38[/m]
Ответ: 38