Задача 78337 Решить управления на картинке ...
Условие
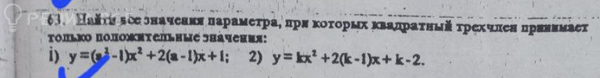
Решение
1) y = (a^2 - 1)*x^2 + 2(a - 1)*x + 1
При a = 1 будет:
y = (1 - 1)*x^2 + 2(1 - 1)*x + 1 = 1
Поэтому [b]a1 = 1[/b] - это решение.
При a = -1 будет:
y = (1 - 1)*x^2 + 2(-1 - 1)*x + 1 = -2x + 1
Это прямая, которая принимает отрицательные значения при x > 1/2
Поэтому a = -1 - это НЕ решение.
Далее, квадратный трехчлен принимает только положительные значения при условиях:
Коэффициент при x^2 больше 0 и Дискриминант меньше 0.
{ a^2 - 1 > 0
{ 4(a - 1)^2 - 4(a^2 - 1)*1 < 0
Раскрываем скобки:
{ (a + 1)(a - 1) > 0
{ 4a^2 - 8a + 4 - 4a^2 + 4 < 0
Приводим подобные:
{ a ∈ (-oo; -1) U (1; +oo)
{ -8a + 8 < 0
Решаем:
{ a ∈ (-oo; -1) U (1; +oo)
{ a > 1
[b]a2 ∈ (1; +oo)[/b]
Ответ: [b]a ∈ [1; +oo)[/b]
2) y = k*x^2 + 2(k - 1)*x + (k - 2)
При k = 0 будет:
y = 0*x^2 + 2(-1)*x + (-2) = -2x - 2
Это прямая, которая принимает отрицательные значения при x > -1
Поэтому k = 0 - это НЕ решение.
Далее, квадратный трехчлен принимает только положительные значения при условиях:
Коэффициент при x^2 больше 0 и Дискриминант меньше 0.
{ k > 0
{ 4(k - 1)^2 - 4k(k - 2) < 0
Раскрываем скобки:
{ k > 0
{ 4k^2 - 8k + 4 - 4k^2 + 8k < 0
Приводим подобные:
{ k > 0
{ 4 < 0
Последнее неравенство не выполняется ни при каком k, поэтому
Ответ: [b]Решений нет.[/b]