Задача 78325 В равнобедренную трапецию вписана...
Условие
Решение
Дана равнобедренная трапеция ABCD,
В нее вписана окружность, центр O, радиус R = 4
S(тр) = 128
Окружность касается сторон в точках M, N, K, L.
Найти: |MN|
Решение.
Так как R = 4, то высота трапеции
H = |KL| = D = 2R = 8
Так как трапеция равнобедренная и в неё вписана окружность, то:
|AL| = |BL| = |AM| = |BN|
|DK| = |CK| = |DM| = |CN|
Площадь трапеции:
[m]S(тр) = \frac{(|AB| + |CD|) \cdot H}{2} = 128[/m]
[m]\frac{(|AL|+|BL|+|DK|+|CK|) \cdot 8}{2} = 128[/m]
[m]2|AL| + 2|DK| = \frac{128}{4} = 32[/m]
|AL| + |DK| = 16
Но |AL| = |AM|, |DK| = |DM|, поэтому:
|AM| + |DM| = |AD| = |BC| = 16
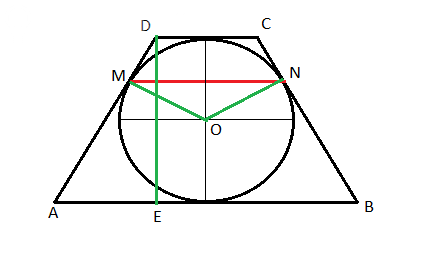
Проведем высоту DE. Она показана зеленым цветом.
В прямоугольном треугольнике ADE
катет DE = 8, гипотенуза AD = 16, значит, угол ∠ А = 30°.
Потому что катет против угла 30° равен половине гипотенузы.
Проведем радиусы OM и ON. Они тоже показаны зеленым цветом.
Они перпендикулярны к сторонам:
OM ⊥ AD, ON ⊥ BC
Так как MN || AB || CD, то углы наклона равны:
∠ DMN = ∠ A = 30°
Угол ∠ AMD = 180° - развернутый.
Тогда угол:
∠ NMO = ∠ AMD - ∠ AMO - ∠ DMN = 180° - 90° - 30° = 60°
А так как треугольник MNO - равнобедренный и ∠ NMO = 60°,
то этот треугольник MNO - равносторонний.
|MN| = |OM| = |ON| = R = 4
Ответ: 4