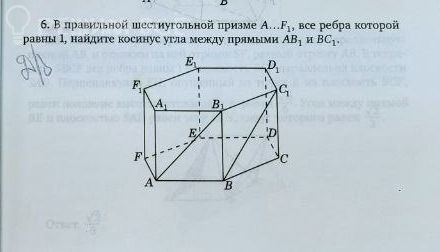
Задача 78218 В правильной шестиугольной призме А…F1,...

66eaf3515974c737d5812bda

9/18/2024 3:36:55 PM

В правильной шестиугольной призме А…F1, все ребра которой равны 1, найдите косинус угла между прямыми АВ1 и ВС1

626fab9a354ab65fb2f43abb

9/19/2024 5:38:00 PM

★

Построим сверху на этой призме ещё одну такую же призму на высоте 1.
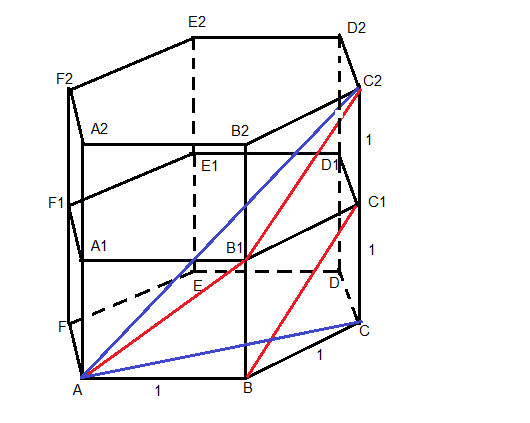
Смотрите рисунок. Нужные отрезки я нарисовал красным, а [AC2] синим.
|AB| = |BC| = |CC1| = |C1C2| = 1 по условию.
|AB1| = |BC1| = |B1C2| = sqrt(2)
Угол ∠ ABC = 120° = 2π/3
От того, что мы переносим отрезок [BC1] в отрезок [B1C2],
угол между отрезками [AB1] и [BC1] - не поменяется.
Получили угол ∠ AB1C2, косинус которого надо найти.

По теореме косинусов для треугольника Δ ABC:
|AC|^2 = |AB|^2 + |BC|^2 - 2*|AB|*|BC|*cos ABC = 1^2 + 1^2 - 2*1*1*(-1/2) = 3
|AC| = sqrt(3)

По теореме Пифагора для треугольника Δ ACC2:
|AC2|^2 = |AC|^2 + |CC2|^2 = 3 + 2^2 = 3 + 4 = 7
|AC2| = sqrt(7)

По теореме косинусов для треугольника Δ AB1C2:
|AC2|^2 = |AB1|^2 + |B1C2|^2 - 2*|AB1|*|B1C2|*cos (AB1C2)
7 = 2 + 2 - 2*sqrt(2)*sqrt(2)*cos (AB1C2)
2*2*cos (AB1C2) = 4 - 7 = -3
cos (AB1C2) = -3/4 = -0,75

Ответ: -0,75