Задача 78165 1) расстояние от точки D до каждой из...

66e0869a5974c737d5812273

9/10/2024 6:02:49 PM

1) расстояние от точки D до каждой из вершин равностороннего треугольника ABC равно 4 см. AB = 6 см. найдите расстояние от точки М до плоскости ABC.
A) 2 см B) 4 см C) 3 см D) 6 см

626fab9a354ab65fb2f43abb

9/10/2024 7:28:42 PM

★

Смотрите рис. 1
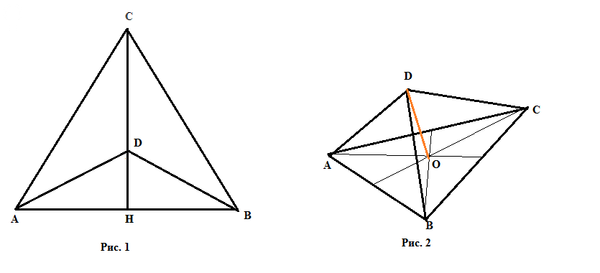
Предположим, что точка D лежит в той же плоскости ABC.
Тогда высота CH = a*sqrt(3)/2 = 6*sqrt(3)/2 = 3*sqrt(3) см
CD = 2/3*CH = 2/3*3*sqrt(3) = 2*sqrt(3) см < 4 см
Значит, точка D находится выше плоскости ABC.
Смотрите рис. 2
Треугольник COD - прямоугольный,
CO = 2*sqrt(3) см, CD = 4 см по условию,
Расстояние от точки D до плоскости ABC:
OD^2 = CD^2 - CO^2 = 4^2 - 2^2*3 = 16 - 12 = 4
OD = sqrt(4) = 2 см.

Ответ: А) 2 см