Задача 78099 При каких значениях параметра а...
Условие
Решение
[m]a=\frac{|6-2x^3|}{log_{\frac{4}{3}}|6-2x^3|}[/m]
[b]Замена переменной:[/b]
[m]t=6-2x^3[/m]
Решаем графически.
Строим два графика:
[m]y=\frac{|t|}{log_{\frac{4}{3}}|t|}[/m]
[m]y=a[/m]
[b]Исследуем функцию [/b]
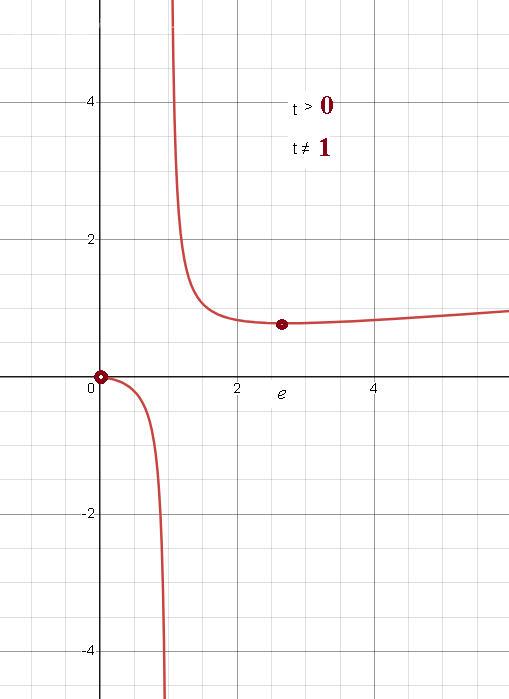
[m]y=\frac{t}{log_{\frac{4}{3}}t}[/m]
при t >0
t ≠ 1
[b] c помощью производной[/b]
[m]y`=\frac{(t)`\cdot log_{\frac{4}{3}}t-t\cdot( log_{\frac{4}{3}}t)`}{log^2_{\frac{4}{3}}t}[/m]
[m]y`=\frac{(t)`\cdot log_{\frac{4}{3}}t-t\cdot \frac{1}{t\cdot ln\frac{4}{3}}}{log^2_{\frac{4}{3}}t}[/m]
[m]y`=\frac{ log_{\frac{4}{3}}t-\frac{1}{ ln\frac{4}{3}}}{log^2_{\frac{4}{3}}t}[/m]
[m]y`=\frac{ log_{\frac{4}{3}}t- log_{\frac{4}{3}}e}{log^2_{\frac{4}{3}}t}[/m] ⇒ t=e - точка минимума ⇒
[m]y(e)=\frac{e}{log_{\frac{4}{3}}e}[/m]
[m]y(e)=e\cdot ln\frac{4}{3}[/m]
Cм. график при t>0; t ≠ 1
В силу симметрии график [m]y=\frac{|t|}{log_{\frac{4}{3}}|t|}[/m] получаем из построенного с помощью симметрии относительно оси Оу
Уравнение имеет ровно два решения, если прямая y=a пересекает график ровно в двух точках
⇒ При [m]a <0[/m] и [m] a=e\cdot ln\frac{4}{3}[/m][/m]
О т в е т. При [m]a <0[/m] ; [m] a=e\cdot ln\frac{4}{3}[/m][/m]