Задача 78079 ...
Условие
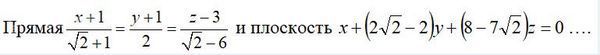
Решение
Плоскость [m]x+(2\sqrt{2}-2)y + (8-7\sqrt{2})z = 0[/m]
Видимо, нужно понять, каково взаимное расположение прямой и плоскости.
Проверим расположение направляющего вектора прямой [m](\sqrt{2}+1; 2; \sqrt{2}-6)[/m] и нормального вектора плоскости [m](1; 2\sqrt{2}-2; 8-7\sqrt{2})[/m]
На пропорциональность: [m]\frac{A}{m} = \frac{B}{n} = \frac{C}{p} = k[/m]
Здесь [m]A = 1; B = 2\sqrt{2}-2; C = 8-7\sqrt{2}[/m] - коэффициенты при x, y, z у плоскости.
[m]m = \sqrt{2}+1; n = 2; p = \sqrt{2}-6[/m] - коэффициенты при x, y, z у прямой.
[m]\frac{A}{m} = \frac{1}{\sqrt{2}+1} = \frac{\sqrt{2}-1}{(\sqrt{2}+1)(\sqrt{2}-1)} = \frac{\sqrt{2}-1}{2-1} = \sqrt{2}-1[/m]
[m]\frac{B}{n} = \frac{2\sqrt{2}-2}{2} = \frac{\sqrt{2}-1}{1} = \sqrt{2}-1[/m]
[m]\frac{C}{p} = \frac{8-7\sqrt{2}}{\sqrt{2}-6} = \frac{(8-7\sqrt{2})(\sqrt{2}+6)}{(\sqrt{2}-6)(\sqrt{2}+6)} = \frac{8\sqrt{2} - 7\sqrt{2} \cdot \sqrt{2} + 8 \cdot 6 - 7\sqrt{2} \cdot 6}{2 - 36} =[/m]
[m]= \frac{8\sqrt{2} - 14 + 48 - 42\sqrt{2}}{- 34} = \frac{34 - 34\sqrt{2}}{- 34} = \frac{1 - \sqrt{2}}{- 1} = \sqrt{2} - 1[/m]
[m]k = \sqrt{2}-1[/m]
Так как коэффициенты пропорциональны, то направляющий вектор прямой и нормальный вектор плоскости - параллельны друг другу.
Это значит, что плоскость и прямая перпендикулярны друг другу.