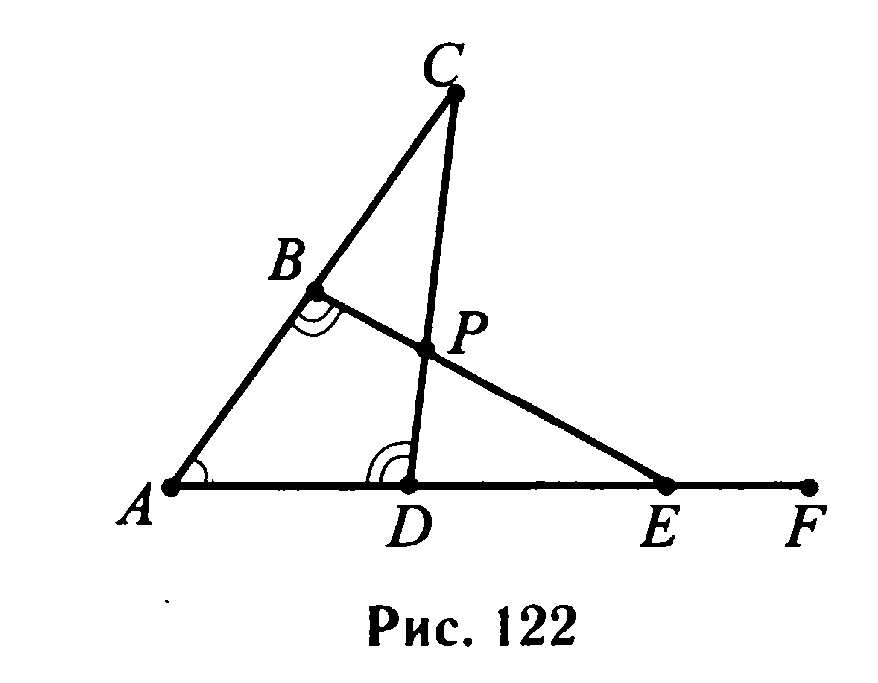
На рисунке 122 выполняется ∠CAE = 40°, ∠ABP = ∠ADP, ∠BEF = 140°. Найдите величину ∠BPD в градусах.
математика 8-9 класс
14310
∠BEF внешний угол треугольника ABE, внешний угол треугольника равен сумме не смежных с ним внутренних углов треугольника, т.е ∠BEF=∠BAE+∠ABE => ∠ABP=140-40=100 => ∠ADP=100. Сумма внутренних углов выпуклого четырехугольника равна 360 => ∠BPD=360-200-40=120
Ответ: 120
Вопросы к решению (3)
угол BEF внешний угол треугольника АВЕ. Внешний угол треугольника равен сумме несмежных с ним углов: ∠BEF=∠BAE+∠ABE => ∠ABP=∠BEF-∠BAE => ∠ABP=140–40=100

