Задача 78028 ...
Условие
Решение

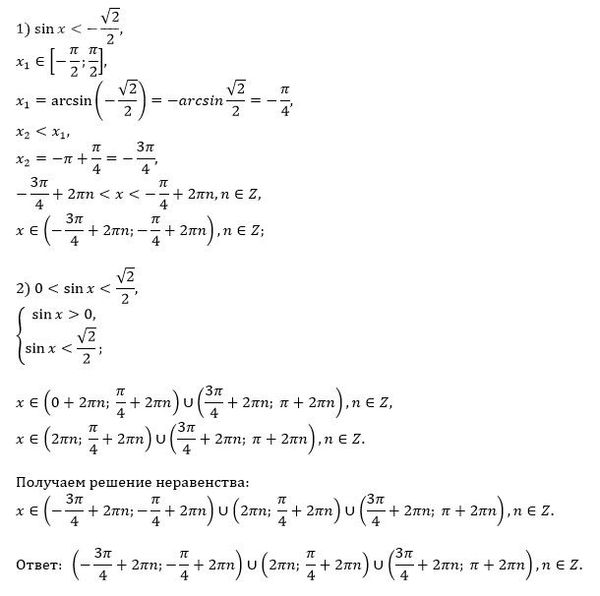
Все решения
sin x < 2sin x*cos x*cos x
sin x - 2sin x*cos^2 x < 0
sin x*(1 - 2cos^2 x) < 0
Если произведение двух чисел меньше 0, то числа имеют разные знаки.
1)
{ sin x < 0
{ 1 - 2cos^2 x > 0
Решаем:
{ x ∈ (-π + 2π*n; 2π*n); n ∈ Z
{ cos^2 x < 1/2
Это эквивалентно такой системе:
{ x ∈ (-π + 2π*n; 2π*n); n ∈ Z
{ x ∈ (π/4 + 2π*k; 3π/4 + 2π*k) U (5π/4 + 2π*k; 7π/4 + 2π*k); k ∈ Z
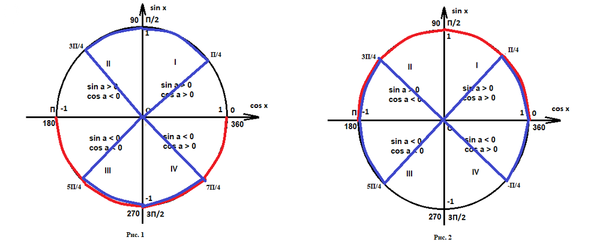
Решение 1 неравенства показано на Рисунке 1 красным.
Решение 2 неравенства показано на Рисунке 1 синим.
Решение системы:
x ∈ (5π/4 + 2π*k; 7π/4 + 2π*k); k ∈ Z
2)
{ sin x > 0
{ 1 - 2cos^2 x < 0
Решаем:
{ x ∈ (2π*n; π + 2π*n); n ∈ Z
{ cos^2 x > 1/2
Это эквивалентно такой системе:
{ x ∈ (2π*n; π + 2π*n); n ∈ Z
{ x ∈ (-π/4 + 2π*k; π/4 + 2π*k) U (3π/4 + 2π*k; 5π/4 + 2π*k); k ∈ Z
Решение 1 неравенства показано на Рисунке 2 красным.
Решение 2 неравенства показано на Рисунке 2 синим.
Решение системы:
x ∈ (2π*k; π/4 + 2π*k) U (3π/4 + 2π*k; π + 2π*k); k ∈ Z
Ответ:
[b](2π*k; π/4 + 2π*k) U (3π/4 + 2π*k; π + 2π*k) U (5π/4 + 2π*k; 7π/4 + 2π*k)[/b]