Задача 77978 Решить неравенство 2 log_3 x-log_1/3...
Условие
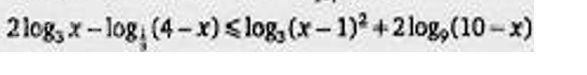
Решение
Область определения функции логарифма:
{ x > 0
{ 4 - x > 0
{ (x - 1)^2 > 0
{ 10 - x > 0
Решаем:
{ x > 0
{ x < 4
{ x ≠ 1
{ x < 10
Получаем:
x ∈ (0; 1) U (1; 4)
Приведем все основания логарифмов к одному основанию 3:
[m]\log_{1/3} (4-x) = -\log_3 (4-x);\ \ \ \log_9 (10-x) = \frac{1}{2} \cdot \log_3 (10-x);[/m]
[m]2\log_9 (10-x) = 2 \cdot \frac{1}{2} \cdot \log_3 (10-x) = \log_3 (10-x);\ \ \ 2\log_3 x = \log_3 x^2[/m]
Подставляем:
[m]\log_3 x^2 + \log_3 (4-x) ≤ \log_3 (x-1)^2 + \log_3 (10-x)[/m]
Сумма логарифмов равна логарифму произведения:
[m]\log_3 (x^2(4-x)) ≤ \log_3 ((x-1)^2(10-x))[/m]
Так как 3 > 1, то функция log_3(x) - возрастающая.
Чем больше выражение под логарифмом, тем больше сам логарифм.
Это значит, что при переходе от логарифмов к выражениям под логарифмами знак неравенства не изменится.
x^2(4 - x) ≤ (x^2 - 2x + 1)(10 - x)
4x^2 - x^3 ≤ 10x^2 - 20x + 10 - x^3 + 2x^2 - x
0 ≤ 10x^2 - 4x^2 + 2x^2 - 20x - x + 10
8x^2 - 21x + 10 ≥ 0
D = (-21)^2 - 4*8*10 = 441 - 320 = 121 = 11^2
x1 = (21 - 11)/16 = 10/16 = 5/8
x2 = (21 + 11)/16 = 32/16 = 2
Решение этого квадратного неравенства:
x ∈ (-oo; 5/8] U [2; +oo)
С учетом области определения решение исходного неравенства:
x ∈ (0; 5/8] U [2; 4)