Задача 77937 (log_{2}(2-x)-log_{2}(x+1))/(log^2_{2)(x^2)+log_{2}(x^4)+1}>=0...
Условие
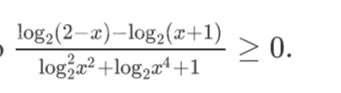
Решение
Область определения функции логарифма:
{ 2 - x > 0
{ x + 1 > 0
{ x ≠ 0
Получаем:
{ x > -1
{ x < 2
{ x ≠ 0
Область определения дроби:
[m]\log_2^2 x^2 + \log_2 x^4 + 1 ≠ 0[/m]
[m](\log_2 x^2)^2 + 2\log_2 x^2 + 1 ≠ 0[/m]
Замена [m]y = \log_2 x^2[/m]
y^2 + 2y + 1 ≠ 0
(y + 1)^2 ≠ 0
y ≠ -1
[m]\log_2 x^2 ≠ -1[/m]
x^2 ≠ 2^(-1)
x^2 ≠ 1/2
x ≠ ± 1/sqrt(2)
Итого получаем область определения:
x ∈ (-1; -1/sqrt(2)) U (-1/sqrt(2); 0) U (0; 1/sqrt(2)) U (1/sqrt(2); 2)
Теперь решаем само неравенство.
В знаменателе, как мы уже выяснили, стоит квадрат:
[m]\log_2^2 x^2 + \log_2 x^4 + 1 = (\log_2 x^2 + 1)^2[/m]
Поэтому он всегда неотрицательный. Значит, числитель тоже неотрицательный.
[m]\log_2 (2-x) - \log_2 (x+1) ≥ 0[/m]
Разность логарифмов равна логарифму дроби:
[m]\log_2 \frac{2-x}{x+1} ≥ 0[/m]
[m]\log_2 \frac{2-x}{x+1} ≥ \log_2 1[/m]
Так как 2 > 1, то функция логарифма по основанию 2 - возрастающая.
Значит, чем больше логарифм, тем больше выражение под логарифмом.
[m]\frac{2-x}{x+1} ≥ 1[/m]
[m]\frac{2-x}{x+1} - 1 ≥ 0[/m]
[m]\frac{2-x - x - 1}{x+1} ≥ 0[/m]
[m]\frac{1-2x}{x+1} ≥ 0[/m]
x ∈ (-1; 1/2]
1/sqrt(2) ≈ 0,707 > 1/2, поэтому с учетом области определения:
Ответ: x ∈ (-1; -1/sqrt(2)) U (-1/sqrt(2); 0) U (0; 1/2]