Задача 77928 ...
Условие
yn=4n3−2n2+9n−28+2n+9n2−n3+8n−3n+2
при n→∞
Если предел не существует, введите слово нет. Если предел бесконечен, введите бск.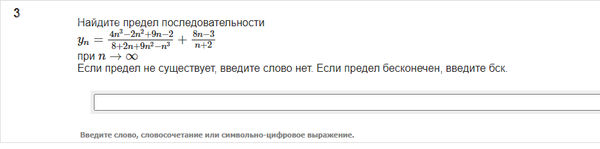
Решение
Можно найти сумму этих дробей, а потом посчитать предел.
Но можно сделать проще. Находим сразу предел этой суммы при n → oo:
[m]\lim \limits_{n \to \infty}(\frac{4n^3-2n^2+9n-2}{-n^3+9n^2+2n+8} + \frac{8n-3}{n+2}) [/m]
Делим в каждой дроби числитель и знаменатель на n в старшей степени.
В 1 дроби делим на n^3, а во 2 дроби на n:
[m]= \lim \limits_{n \to \infty}(\frac{4-2/n+9/n^2-2/n^3}{-1+9/n+2/n^2+8/n^3} + \frac{8-3/n}{1+2/n}) = \frac{4+0-0+0}{-1+0+0+0} + \frac{8+0}{1+0} = \frac{4}{-1} + \frac{8}{1}= 4[/m]