Задача 77918 Установить, является ли данная функция...
Условие
точках х1, x2,. В случае разрыва функции найти ее пределы в точке разрыва слева и справа.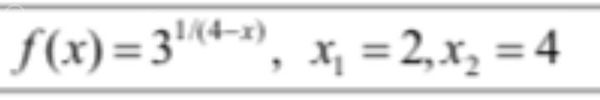
математика ВУЗ
274
Решение
★
В точке x1 = 2 функция непрерывна:
[m]f(2) = 3^{\frac{1}{4-2}} = 3^{\frac{1}{2}} = \sqrt{3}[/m]
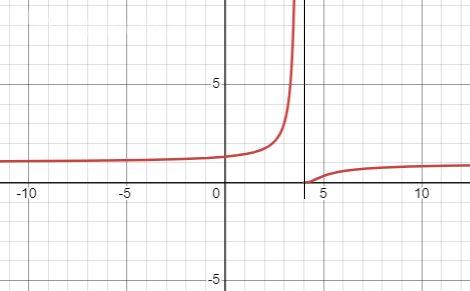
В точке x2 = 4 неустранимый разрыв II рода, уход в бесконечность.
Предел слева:
[m]\lim \limits_{x \to 4-0} 3^{\frac{1}{4-4+0}} = 3^{\frac{1}{+0}} = 3^{+\infty} = +\infty[/m]
Предел справа:
[m]\lim \limits_{x \to 4+0} 3^{\frac{1}{4-4-0}} = 3^{\frac{1}{-0}} = 3^{-\infty} = 0[/m]
График прилагается.
Асимптота x = 4 показана тонкой линией.