Задача 77909 вычислите производные функции ...
Условие
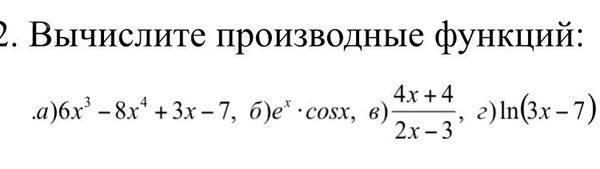
математика колледж
272
Решение
★
б) (e^(x)*cos x)' = (e^(x))'*cos x + e^(x)*(cos x)' = e^(x)*cos x + e^(x)(-sin x) = e^(x)*(cos x - sin x)
в) [m](\frac{4x+4}{2x-3})' = \frac{(4x+4)'(2x-3) - (4x+4)(2x-3)'}{(2x-3)^2} = \frac{4(2x-3) - 2(4x+4)}{(2x-3)^2} = \frac{8x-12 - 8x-8}{(2x-3)^2} = \frac{-20}{(2x-3)^2}[/m]
г) [m](\ln(3x-7))' = \ln'(3x-7) \cdot (3x-7)' = \frac{1}{3x-7} \cdot 3 = \frac{3}{3x-7}[/m]