Задача 77908 ...
Условие
[m] f(x) = 3x^4 - 2x^3 - 36x + 3 [/m] на отрезке [m][-2, 2][/m]
---
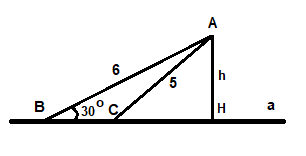
3. Из точки А к плоскости α проведены две наклонные. Первая равна 6см и составляет с плоскостью угол 30°, вторая равна 5см. Найдите проекции наклонных на плоскость α.
---
Даны векторы [m] a = (3, 1, 2), b = (4, -3, 1) [/m]. Найдите координаты вектора [m] c [/m], если [m] c = -3a + 2b [/m].
---
3. 1) Найдите область определения функций:
a) y = cos x + 5x^2, b) y = √(x^2 - 9) / √(2x + 6), c) y = log_3 (x^2 - 5x).

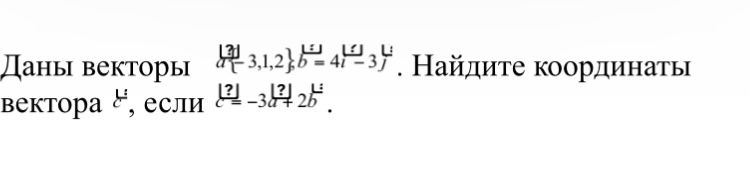
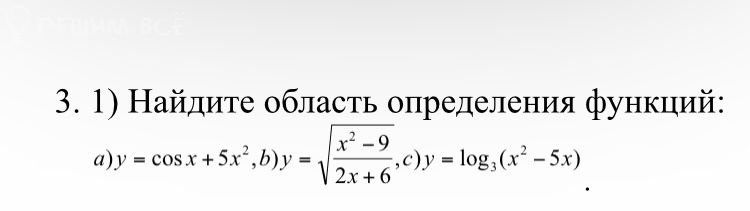
Решение
Значения функции на концах отрезка:
f(-2) = 3(-2)^2 - 2(-2)^3 - 36(-2) + 3 = 3*4 - 2(-8) + 72 + 3 = 103
f(2) = 3*2^2 - 2*2^3 - 36*2 + 3 = 3*4 - 2*8 - 72 + 3 = -73
Находим точки экстремумов:
f'(x) = 0
3*2x - 2*3x^2 - 36 = 0
6x - 6x^2 - 36 = 0
-6(x^2 - x + 6) = 0
D = (-1)^2 - 4*1*6 = -1 - 24 = -25 < 0
Уравнение в скобках решений не имеет, значит, экстремумов нет.
При любом x будет f'(x) < 0, функция убывает.
Ответ: Наибольшее значение: f(-2) = 103; наименьшее значение f(2) = -73
2) Смотрите рисунок.
h = AH = 6*sin 30° = 6*0,5 = 3 см.
Если вы не знаете синусов, то можно вспомнить теорему:
Катет против угла 30° равен половине гипотенузы.
Проекции находим из теоремы Пифагора:
BH^2 = AB^2 - AH^2 = 6^2 - 3^2 = 36 - 9 = 27
BH = sqrt(27) = 3sqrt(3) см
CH^2 = AC^2 - AH^2 = 5^2 - 3^2 = 25 - 9 = 16
CH = 4 см.
3) a{-3; 1; 2} = -3i + j + 2k; b = 4i - 3j
c = -3a + 2b = -3(-3i + j + 2k) + 2(4i - 3j) = 9i - 3j - 6k + 8i - 6j = 17i - 9j - 6k
c{17; -9; -6}
4) a) y = cos x + 5x^2
D(X) = R
b) [m]y=\sqrt{\frac{x^2-9}{2x+6}}[/m]
{ [m]\frac{x^2-9}{2x+6} ≥ 0[/m]
{ 2x + 6 ≠ 0
Решаем:
{ [m]\frac{(x-3)(x+3)}{2(x+3)} ≥ 0[/m]
{ 2(x + 3) ≠ 0
Сокращаем:
{ [m]\frac{x-3}{2} ≥ 0[/m]
{ x + 3 ≠ 0
Получаем:
{ x ≥ 3
{ x ≠ -3
D(X) = [3; +oo)
c) [m]y = \log_3 (x^2-5x)[/m]
x^2 - 5x > 0
x(x - 5) > 0
D(X) = (-oo; 0) U (5; +oo)