Задача 77905 6. В правильной четырехугольной пирамиде...

667bb69f4a6eb928f58e6af3

6/26/2024 6:36:18 AM

6. В правильной четырехугольной пирамиде боковое ребро равно 25, сторона основания равна 2442 Найдите объем пирамиды.

626fab9a354ab65fb2f43abb

6/26/2024 2:44:34 PM

★

Если пирамида правильная и 4-угольная, то в основании лежит квадрат.
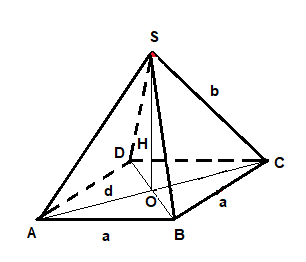
Сторона основания a = 24sqrt(2), а боковое ребро b = 25.
Смотрите рисунок.
S(осн) = a^2 = (24sqrt(2))^2 = 576*2 = 1152
d = AC = a*sqrt(2) = 24sqrt(2)*sqrt(2) = 24*2 = 48
OC = d/2 = 48/2 = 24
Треугольник OSC - прямоугольный, по теореме Пифагора:
H = OS = sqrt(SC^2 - OC^2) = sqrt(25^2 - 24^2) = sqrt(625 - 576) = sqrt(49) = 7
Объём пирамиды:
V = 1/3*S(осн)*H = 1/3*1152*7 = 384*7 = 2688
Посчитано в уме, без калькулятора!