Задача 77903 решить пределы...
Условие
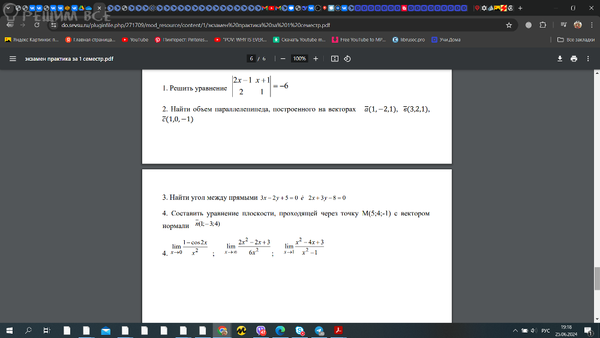
математика ВУЗ
271
Решение
★
Дальше решаете по 1 Замечательному пределу.
[m]\lim \limits_{x \to 0} \frac{\sin x}{x} = 1[/m]
2) [m]\lim \limits_{x \to \infty} \frac{2x^2-2x+3}{6x^2} = \lim \limits_{x \to \infty} \frac{2-2/x+3/x^2}{6} = \frac{2-0+0}{6}[/m]
Закончите сами
3) [m]\lim \limits_{x \to 1} \frac{x^2-4x+3}{x^2-1} = \lim \limits_{x \to 1} \frac{(x-1)(x-3)}{(x-1)(x+1)} = \lim \limits_{x \to 1} \frac{x-3}{x+1} = \frac{1-3}{1+1} [/m]
Закончите сами