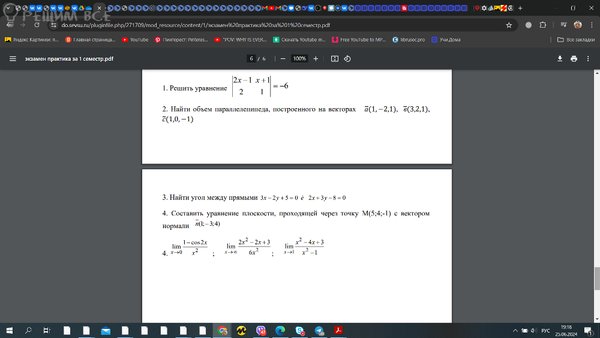
Задача 77900 Найти объем параллелепипеда,...
Условие
Решение
Найдем длину каждого вектора:
|a| = sqrt(1^2 + (-2)^2 + 1^2) = sqrt(1 + 4 + 1) = sqrt(6)
|b| = sqrt(3^2 + 2^2 + 1^2) = sqrt(9 + 4 + 1) = sqrt(14)
|c| = sqrt(1^2 + 0^2 + (-1)^2) = sqrt(1 + 0 + 1) = sqrt(2)
Найдем углы между векторами:
[m]\cos (a; b) = \frac{x(a) \cdot x(b) + y(a) \cdot y(b) + z(a) \cdot z(b)}{|a| \cdot |b|} = \frac{1 \cdot 3 + (-2) \cdot 2 + 1 \cdot 1}{\sqrt{6} \cdot \sqrt{14}} = \frac{3 - 4 + 1}{\sqrt{84}} = 0[/m]
cos (a; b) = 0, значит, ∠ (a; b) = π/2
В основании параллелепипеда лежит прямоугольник, значит, площадь основания:
S(осн) = |a|*|b| = sqrt(6)*sqrt(14) = sqrt(84)
[m]\cos (b; c) = \frac{x(b) \cdot x(c) + y(b) \cdot y(c) + z(b) \cdot z(c)}{|b| \cdot |c|} = \frac{3 \cdot 1 + 2 \cdot 0 + 1 \cdot (-1)}{\sqrt{14} \cdot \sqrt{2}} = \frac{3 + 0 - 1}{\sqrt{28}} = \frac{2}{\sqrt{28}} = \frac{1}{\sqrt{7}}[/m]
[m]\sin (b;c) = \sqrt{1 - \cos^2 (b;c)} = \sqrt{1 - \frac{1}{7}} = \sqrt{\frac{6}{7}} = \frac{\sqrt{42}}{7}[/m]
Высота параллелепипеда равна боковому ребру, умноженному на синус угла:
[m]H = |c| \cdot \sin (b;c) = \sqrt{2} \cdot \frac{\sqrt{42}}{7} = \frac{\sqrt{84}}{7}[/m]
Объем параллелепипеда:
V = S(осн)*H = sqrt(84)*sqrt(84)/7 = 84/7 = 12
Ответ: 12