Задача 77882 Вычислить значения частных производных ...
Условие
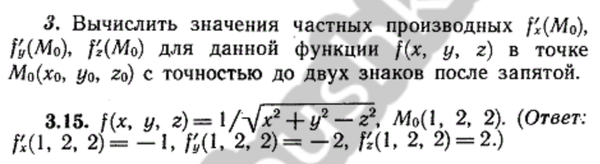
математика ВУЗ
270
Решение
★
[m]f'_{x} = -\frac{1}{2}(x^2+y^2-z^2)^{-3/2} \cdot 2x = -\frac{x}{(x^2+y^2-z^2)^{3/2}}[/m]
[m]f'_{x}(M0) = -\frac{1}{(1^2+2^2-2^2)^{3/2}} = -\frac{1}{(1)^{3/2}} = -1[/m]
[m]f'_{y} = -\frac{1}{2}(x^2+y^2-z^2)^{-3/2} \cdot 2y = -\frac{y}{(x^2+y^2-z^2)^{3/2}}[/m]
[m]f'_{y}(M0) = -\frac{2}{(1^2+2^2-2^2)^{3/2}} = -\frac{2}{(1)^{3/2}} = -2[/m]
[m]f'_{z} = -\frac{1}{2}(x^2+y^2-z^2)^{-3/2} \cdot (-2z) = \frac{z}{(x^2+y^2-z^2)^{3/2}}[/m]
[m]f'_{z}(M0) = \frac{2}{(1^2+2^2-2^2)^{3/2}} = \frac{2}{(1)^{3/2}} = 2[/m]