Задача 77880 ...

wooooow

22 июня 2024 г. в 07:55

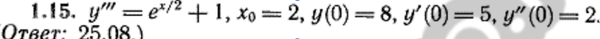
Найти частное решение дифференциального уравнения и вычислить значение полученной функции y=φ(x) при x=x0 с точностью до двух знаков после запятой.

Удачник66

22 июня 2024 г. в 09:15

★

y''' = e^x/2 + 1; x₀ = 2; y(0) = 8; y'(0) = 5; y''(0) = 2
Просто берем интегралы три раза.
[m]y'' = \int (e^{x/2} + 1)\ dx = 2e^{x/2} + x + C1[/m]
[m]y' = \int (2e^{x/2} + x + C1)\ dx = 4e^{x/2} + \frac{x^2}{2} + C1x + C2[/m]
[m]y = \int (4e^{x/2} + \frac{x^2}{2} + C1x + C2)\ dx = 8e^{x/2} + \frac{x^3}{6} + \frac{C1x^2}{2} + C2x + C3[/m]
Решаем задачу по начальным условиям: x₀ = 2
[m]y(0) = 8e^{0} + \frac{0}{6} + \frac{C1 \cdot 0}{2} + C2 \cdot 0 + C3 = 8[/m]
[m]8 + C3 = 8[/m] (1)
[m]y'(0) = 4e^{0} + \frac{0}{2} + C1 \cdot 0 + C2 = 5[/m]
[m]4 + C2 = 5[/m] (2)
[m]y''(0) = 2e^{0} + 0 + C1 = 2[/m]
[m]2 + C1 = 2[/m] (3)

Уравнения (1), (2), (3) собираем в одну систему:
{ 2 + C1 = 2
{ 4 + C2 = 5
{ 8 + C3 = 8
Получаем:
{ C1 = 0
{ C2 = 1
{ C3 = 0
Частное решение:
[m]y(x) = 8e^{x/2} + \frac{x^3}{6} + \frac{0}{2} + 1 \cdot x + 0[/m]
[m]y(x) = 8e^{x/2} + \frac{x^3}{6} + x[/m]
[m]y(x_0) = y(2) = 8e^{2/2} + \frac{2^3}{6} + 2 = 8e + \frac{4}{3} + 2 = [/m]
[m]= 8 \cdot 2,718 + 1,333 + 2 = 21,744 + 3,333 = 25,077 ≈ 25,08[/m]