Задача 77860 при каких значениях параметра а,...
Условие
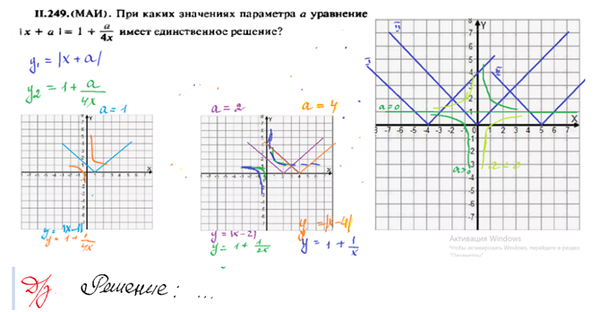
Решение
При каких значениях параметра а уравнение имеет 1 решение?
Рассмотрим две функции:
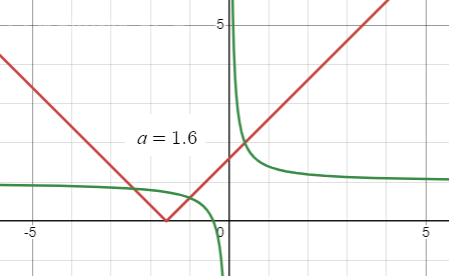
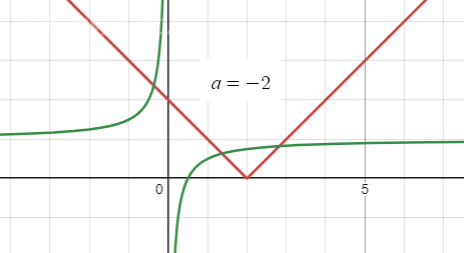
y = |x + a| - два луча, выходящие из точки (-a; 0) и идущие вверх.
y = 1 + a/(4x) - гипербола с асимптотами x = 0, y = 1
Я построил графики при a > 0 и при a < 0.
Получилось, что при любом a ≠ 0 будет 3 решения.
При а = 0 получается:
|x| = 1
Это уравнение имеет 2 решения: x1 = -1; x2 = 1
Попробуем решить аналитически.
Заметим, что x не может быть равен -а. Потому что тогда получается:
|-a + a| = 1 + a/(-4a)
0 = 1 - 1/4
Что явно ложно, поэтому такого быть не может.
1) Пусть x < -a, тогда |x + a| = -x - a
-x - a = 1 + a/(4x)
-4x^2 - 4ax = 4x + a
0 = 4x^2 + 4ax + 4x + a
4x^2 + (4a+4)*x + a = 0
D = (4a+4)^2 - 4*4a = 16a^2 + 32a + 16 - 16a = 16a^2 + 16a + 16 = (4sqrt(a^2+a+1))^2
Выражение под корнем положительно при любом а, поэтому есть 2 решения:
[m]x1 = \frac{-4a - 4 - 4\sqrt{a^2+a+1}}{8} = \frac{-a - 1 - \sqrt{a^2+a+1}}{2}[/m]
[m]x2 = \frac{-4a - 4 + 4\sqrt{a^2+a+1}}{8} = \frac{-a - 1 + \sqrt{a^2+a+1}}{2}[/m]
2) Пусть x > -a, тогда |x + a| = x + a
x + a = 1 + a/(4x)
4x^2 + 4ax = 4x + a
4x^2 + 4ax - 4x - a = 0
4x^2 + (4a-4)*x - a = 0
D/4 = (4a-4)^2 - 4*4(-a) = 16a^2 - 32a + 16 + 16a = 16a^2 - 16a + 16 = (4sqrt(a^2-a+1))^2
Выражение под корнем положительно при любом а, поэтому есть 2 решения:
[m]x3 = \frac{-4a + 4 - 4\sqrt{a^2-a+1}}{8} = \frac{-a + 1 - \sqrt{a^2-a+1}}{2}[/m]
[m]x4 = \frac{-4a + 4 + 4\sqrt{a^2-a+1}}{8} = \frac{-a + 1 + \sqrt{a^2-a+1}}{2}[/m]
У нас получилось в общем случае 4 корня, но на самом деле их будет 3.
При a < 0 будет 2 корня x1 < -a, x2 < -a и 1 корень x3 > -a.
А при a > 0 будет 2 корня x1 > -a, x2 > -a и 1 корень x3 < -a.
Это из-за того, что при каком-то x значение функции справа будет 1 + a/(4x) < 0,
а модуль слева не может быть отрицательным, поэтому один из корней выпадает.
Ответ: НИ ПРИ КАКОМ а это уравнение не имеет единственное решение!