Задача 77859 сколько решений имеет система, в...
Условие
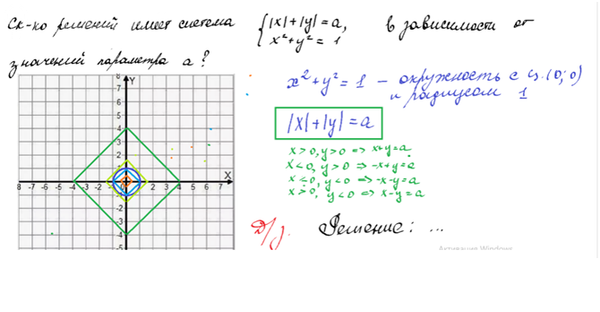
Решение
{ x^2 + y^2 = 1
Решаем алгебраически.
Рассмотрим функцию |x| + |y| = a.
Очевидно, что при a < 0 функция не существует, потому что модули неотрицательны.
При а = 0 решением будет одна точка x = 0, y = 0: O(0, 0)
При a > 0 будет 4 отрезка:
y = -x - a при x < 0, y < 0
y = x - a при x > 0, y < 0
y = -x + a при x > 0, y > 0
y = x + a при x < 0, y > 0
Это получается диагональный квадрат из 4 отрезков.
Заметим, что |x| ≤ a, |y| ≤ a, то есть x ∈ (-a; a); y ∈ (-a; a) при a > 0
Второе уравнение: x^2 + y^2 = 1 - это окружность, O(0; 0); R = 1
Перепишем его так:
y1 = -sqrt(1 - x^2) (при y ≤ 0)
y2 = sqrt(1 - x^2) (при y ≥ 0)
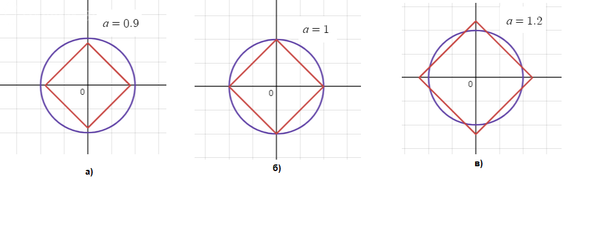
Очевидно, что при a < 1 график 1 уравнения целиком лежит внутри окружности,
поэтому система решений не имеет. Это показано на Рис а).
При а = 1 будет 4 решения: (-1; 0); (1; 0); (0; -1); (0; 1). Это показано на Рис б).
Далее, найдем при каком а прямые будут касаться окружности.
1) x < 0, y < 0
-x - a = -sqrt(1 - x^2)
x + a = sqrt(1 - x^2)
x^2 + 2ax + a^2 = 1 - x^2
2x^2 + 2ax + (a^2 - 1) = 0
D = (2a)^2 - 4*2(a^2 - 1) = 4a^2 - 8a^2 + 8 = 8 - 4a^2 = 4(2 - a^2)
Так как прямая касается окружности, то уравнение имеет 1 решение.
Значит, D = 0
4(2 - a^2) = 0
a^2 = 2
a = sqrt(2)
Значение a = -sqrt(2) не подходит, потому что мы знаем, что a > 0.
Тоже самое получится при решении любого из 4 уравнений:
2) x > 0, y < 0
x - a = -sqrt(1 - x^2)
a - x = sqrt(1 - x^2)
a^2 - 2ax + x^2 = 1 - x^2
3) x > 0, y > 0
-x + a = sqrt(1 - x^2)
a - x = sqrt(1 - x^2)
a^2 - 2ax + x^2 = 1 - x^2
4) x < 0, y > 0
x + a = sqrt(1 - x^2)
x^2 + 2ax + a^2 = 1 - x^2
Таким образом, мы получаем, что при a ∈ (1; sqrt(2)) квадрат и окружность пересекаются в 8 точках, то есть будет 8 решений. Это показано на Рис в).
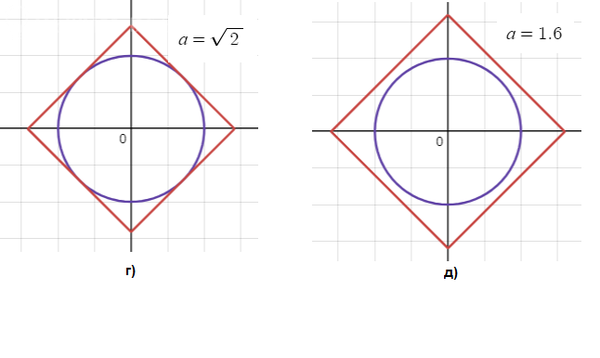
А при a = sqrt(2) будет 4 решения: (-sqrt(2); -sqrt(2)); (-sqrt(2); sqrt(2)); (sqrt(2); -sqrt(2)); (sqrt(2); sqrt(2))
Это показано на Рис г).
И, наконец, при a > sqrt(2) окружность окажется внутри квадрата, и решений опять нет.
Это показано на Рис д).