Задача 77847 ...

6672831e4a6eb928f58e64fd

6/19/2024 7:06:58 AM

В правильной четырехугольной пирамиде боковое ребро, равное 2√2 см,
наклонено к основанию под углом 45°. Вычислите объем пирамиды.

626fab9a354ab65fb2f43abb

6/19/2024 11:51:35 AM

★

Смотрите рисунок.
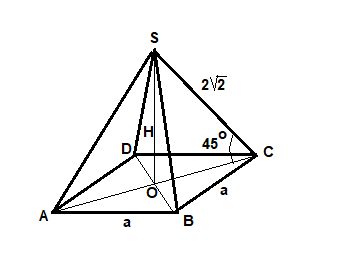
Правильная 4-угольная пирамида ABCDS, в основании квадрат.
Сторона квадрата AB = BC = a см.
Боковое ребро CS = 2sqrt(2) см, высота SO = H см.
Треугольник SOC - прямоугольный и равнобедренный, угол SCO = CSO = 45°.
Значит, катеты SO = OC = CS/sqrt(2) = 2sqrt(2)/sqrt(2) = 2 см.
Высота H = SO = 2 см, диагональ основания AC = 2*OC = 4 см
Сторона основания:
a = AB = BC = AC/sqrt(2) = 4/sqrt(2) = 2sqrt(2) см.
Площадь основания:
S(осн) = a^2 = (2sqrt(2))^2 = 8 см^2
Объем пирамиды:
V = 1/3*S(осн)*H = 1/3*8*2 = 16/3 см^3