Задача 77843 В правильной треугольной пирамиде...

6671dce84a6eb928f58e64bd

6/18/2024 7:18:13 PM

В правильной треугольной пирамиде боковое ребро, равно 6см, наклонено
к основанию под углом 30°. Вычислите объем пирамиды.

626fab9a354ab65fb2f43abb

6/18/2024 7:35:03 PM

★

Сторону основания обозначим а см, позже мы ее вычислим.
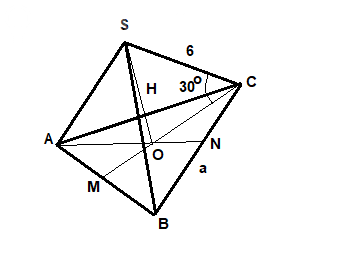
Смотрите рисунок.
Так как пирамида правильная, то основание ABC - равносторонний треугольник.
CM и AN - медианы, они же высоты и биссектрисы, пересекаются в центре O.
Высота пирамиды SO - тоже приходит в этот центр треугольника ABC.
Треугольник SOC - прямоугольный, угол SOC = 90°, угол SCO = 30°.
SO = H = SC*sin SCO = 6*sin 30° = 6*0,5 = 3 см.
CO = SC*cos SCO = 6*cos 30° = 6*sqrt(3)/2 = 3sqrt(3) см.
По свойству медиан в равностороннем треугольнике:
CO = 2/3*CM, поэтому:
CM = 3/2*3sqrt(3) = 9/2*sqrt(3) см.
Но медиана равностороннего треугольника:
m = a*sqrt(3)/2, отсюда:
a = 9/2*sqrt(3) : (sqrt(3)/2) = 9 см
Площадь основания:
S(осн) = a^2*sqrt(3)/4 = 9^2*sqrt(3)/4 = 81/4*sqrt(3) см^2
Объём пирамиды:
V = 1/3*S(осн)*H = 1/3*81/4*sqrt(3)*3 = 81/4*sqrt(3) см^3