Задача 7783 ...
Условие
Решение
-3x+9⩾0.
Решим первое неравенство методом интервалов:
(х^4-81)/(3x^2+8x-3)⩾0;
ОДЗ:
3x^2+8x-3≠0
D=8^2-4*3*(-3)=64+36=100
x1≠(-8+10)/(2*3)≠2/6≠1/3
x2≠(-8-10)/6≠-18/6≠-3
Приравняем числитель к нулю:
х^4-81=0
(x^2-9)(x^2+9)=0
(x-3)(x+3)(x^2+9)=0
1)x-3=0
x=3
или
2)х+3=0
x=-3-не удовл.ОДЗ
или
3) x^2+9=0
х^2=-9 - решений нет
Изобразим на координатной прямой ОДЗ и полученные значения(см.рис.)
Определим знак на каждом интервале, для этого возьмем значение из каждого интервала и подставим в неравенство:
при х=-4 : ((-4)^4-81)/(3*(-4)+8*(-4)-3)=(256-81)/(48-32-3)=175/13
при x=0 : (0-81)/(0+0-3)=(-81)/(-3)=27
при x=1 : (1^4-81)/(3*1^2+8*1-3)(1-81)/(3+8-3)=-80/8=-10
при x=4 : (4^4-81)/(3*4^2+8*4-3)=(256-81)/(48+32-3)=175/77
Значит, решением первого неравенства является x∈(-∞;-3)⋃(-3;1/3)⋃[3;+∞)
Решим второе неравенство:
-3x+9⩾0
-3х⩾-9
х⩽-9:(-3)
х⩽3
Решение второго неравенства является х∈(-∞;3]
Отметим на одной координатной прямой оба решения, решением системы неравенств будет пересечение этих решений(см.рис.)
Решением системы неравенств является
x∈(-∞;-3)⋃(-3;1/3)⋃{3}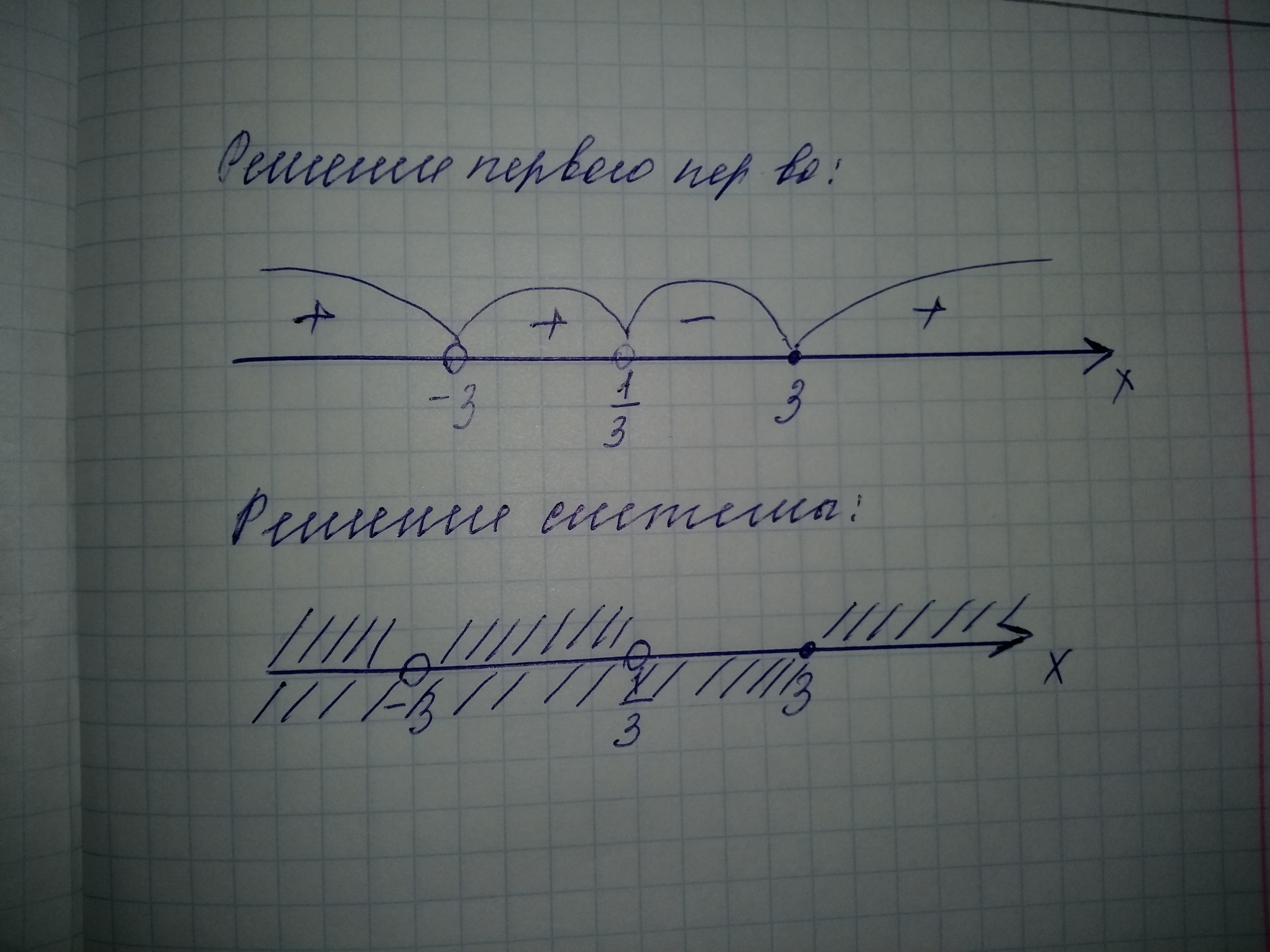
Ответ: (-∞;-3)⋃(-3;1/3)⋃{3}