Задача 77827 ...

666fb52f0d55c3607495d9e9

6/17/2024 4:02:33 AM

Вычислить площадь плоской фигуры ограниченной параболой и прямой
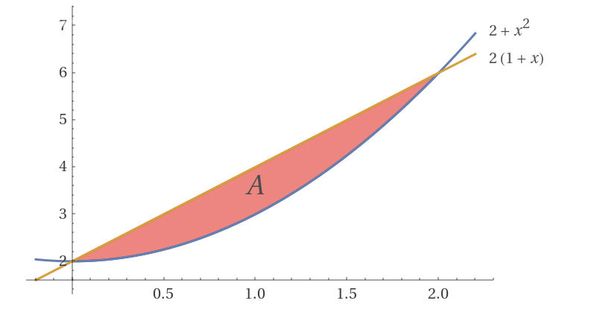
Y=x²+2
y=2x+2

5f282cfba9074b3a3bc0f013

6/17/2024 4:44:04 PM

★

Найдем точки пересечения параболы и прямой.

Приравниваем уравнения:
[m]
x^2 + 2 = 2x + 2
[/m]
Переносим все в одну сторону:
[m]
x^2 - 2x = 0
[/m]
Разложим уравнение на множители:
[m]
x(x - 2) = 0
[/m]
Таким образом, [m] x = 0 [/m] или [m] x = 2 [/m]. Мы получили точки пересечения: [m] (0, 2) [/m] и [m] (2, 6) [/m].

Найдем площадь между кривыми от [m] x = 0 [/m] до [m] x = 2 [/m].
Площадь можно выразить через интеграл, где верхняя функция [m] y = 2x + 2 [/m] и нижняя функция [m] y = x^2 + 2 [/m]:
[m]
A = \int_{0}^{2} [(2x + 2) - (x^2 + 2)] \, dx
[/m]
Упростим подынтегральное выражение:
[m]
A = \int_{0}^{2} (2x + 2 - x^2 - 2) \, dx = \int_{0}^{2} (2x - x^2) \, dx
[/m]

Вычислим интеграл:
[m]
\int_{0}^{2} (2x - x^2) \, dx = \left[ x^2 - \frac{x^3}{3} \right]_{0}^{2}
[/m]
Подставим пределы интегрирования:
[m]
\left[ x^2 - \frac{x^3}{3} \right]_{0}^{2} = \left(2^2 - \frac{2^3}{3}\right) - \left(0^2 - \frac{0^3}{3}\right)
[/m]
Упрощаем выражение:
[m]
= (4 - \frac{8}{3}) - (0)
[/m]
[m]
= 4 - \frac{8}{3}
[/m]
Приведем к общему знаменателю:
[m]
= \frac{12}{3} - \frac{8}{3} = \frac{4}{3}
[/m]

Ответ:
Площадь фигуры, ограниченной параболой [m] y = x^2 + 2 [/m] и прямой [m] y = 2x + 2 [/m], равна [m] \frac{4}{3} [/m] квадратных единиц.