Задача 77823 Решить задачу по аналитической геометрии...
Условие

Решение
Если даны две прямые A1*x + B1*y + C1 = 0 и A2*x + B2*y + C2 = 0, то:
[m]\cos φ = \frac{A1 \cdot A2 + B1 \cdot B2}{\sqrt{A1^2+B1^2}\sqrt{A2^2+B2^2}}[/m]
У нас одна прямая: x + 2y - 1 = 0, другая прямая: ax + by + c = 0, φ = arccos(1/sqrt(5))
Вторая прямая должна находиться на расстоянии s = 1 от точки A(1, 1).
Получаем уравнение:
[m]\cos φ = \frac{1 \cdot a + 2 \cdot b}{\sqrt{1^2+2^2}\sqrt{a^2+b^2}} = \frac{1}{\sqrt{5}}[/m]
[m]\frac{a + 2b}{\sqrt{5}\sqrt{a^2+b^2}} = \frac{1}{\sqrt{5}}[/m]
[m]\frac{a + 2b}{\sqrt{a^2+b^2}} = 1[/m]
[m]a + 2b = \sqrt{a^2+b^2}[/m]
(a + 2b)^2 = a^2 + b^2
a^2 + 4ab + 4b^2 = a^2 + b^2
4ab + 3b^2 = 0
b(4a + 3b) = 0
1) b = 0, тогда прямая имеет вид:
ax + c = 0
x = -c/a - это вертикальна прямая. На расстоянии 1 от точки A(1; 1) будут две прямых:
[b]x = 0 и x = 2[/b] [b](1)[/b]
2) 4a + 3b = 0
4a = -3b
a = 3; b = -4
Уравнение прямой:
3x - 4y + c = 0 [b](2)[/b]
Теперь надо найти, при каких значениях с прямая будет на расстоянии 1 от A(1; 1).
Чтобы найти расстояние от точки до прямой, есть формула:
[m]s=\frac{|A \cdot x0 + B \cdot y0 + C|}{\sqrt{A^2+B^2}}[/m]
В нашем случае A = 3, B = -4, C = c, x0 = 1, y0 = 1:
[m]s=\frac{|3 \cdot 1 + (-4) \cdot 1 + c|}{\sqrt{3^2+(-4)^2}} = \frac{|3 - 4 + c|}{\sqrt{9+16}} = \frac{|-1+ c|}{\sqrt{25}} = \frac{|c-1|}{5} = 1[/m]
Получаем:
|c - 1| = 5
1) c - 1 = -5
c = -4
2) c - 1 = 5
c = 6
Уравнения прямой:
[b]3x - 4y - 4 = 0 и 3x - 4y + 6 = 0[/b]
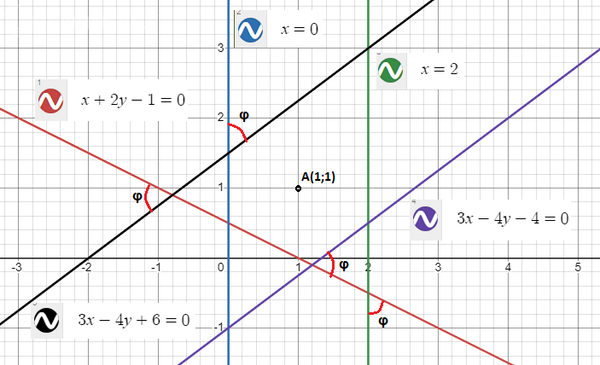
Все прямые, и исходная, и 4 полученных, показаны на рисунке.
Углы φ выделены дугами.
Ответ: 4 прямых:
1) x = 0; 2) x = 2; 3) 3x - 4y - 4 = 0; 4) 3x - 4y + 6 = 0