Задача 77814 Равнобедренная трапеция с основаниями 2...

666d1d6c0d55c3607495d8dc

6/15/2024 4:50:35 AM

Равнобедренная трапеция с основаниями 2 и 3 см и острым углом 60° вращается вокруг меньшего основания. Найдите объем полученной фигуры вращения.

626fab9a354ab65fb2f43abb

6/15/2024 10:08:30 AM

★

Смотрите рисунки.

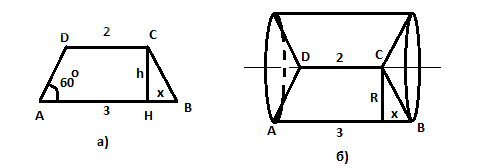
На рис. а) показана трапеция ABCD и ее высота CH = h.
Так как трапеция равнобочная, то:
HB = x = (AB - CD)/2 = (3 - 2)/2 = 1/2 = 0,5
Угол DAH = CBH = 60°.
BC = x/cos 60° = 0,5/0,5 = 1
h = CH = BC*sin 60° = 1*sqrt(3)/2 = sqrt(3)/2

На рисунке б) показано получившееся тело вращения.
Это цилиндр с радиусом R = h = sqrt(3)/2 и высотой H(ц) = AB = 3.
Но в этом цилиндре вырезано два конуса.
Радиус конуса тот же R = h = sqrt(3)/2, а высота конуса H(к) = x = 1/2.
Объем цилиндра:
V(ц) = π*R^2*H(ц) = π*(sqrt(3)/2)^2*3 = π*3/4*3 = π*9/4
Объем конуса:
V(к) = 1/3*π*R^2*H(к) = 1/3*π*(sqrt(3)/2)^2*1/2 = π*1/3*3/4*1/2 = π*1/8
Объем тела вращения:
V = V(ц) - 2*V(к) = π*9/4 - 2*π*1/8 = π*9/4 - π*1/4 = π*8/4 = 2π

Ответ: 2π