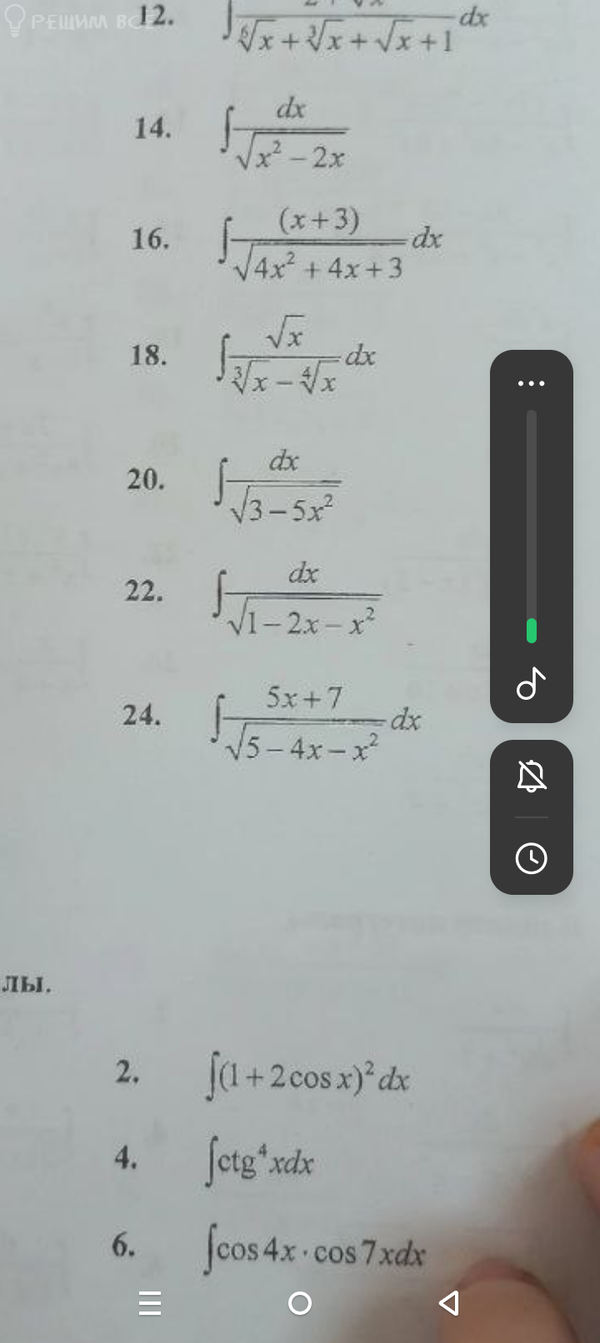
Задача 77761 Надо решить интеграл номер 24...

6654737b3528112db82d8cf9

6/9/2024 3:10:35 PM

Надо решить интеграл номер 24

626fab9a354ab65fb2f43abb

6/9/2024 3:31:41 PM

★

[m]\int \frac{5x+7}{\sqrt{5-4x-x^2}} dx = \int \frac{5x+7}{\sqrt{9-4-4x-x^2}} dx = \int \frac{5x+7}{\sqrt{9-(x+2)^2}} dx =[/m]
[m]\int \frac{5x+10-3}{\sqrt{3^2-(x+2)^2}} dx = \int \frac{5(x+2)-3}{\sqrt{3^2-(x+2)^2}} dx = \int \frac{5(x+2)}{\sqrt{3^2-(x+2)^2}} dx - \int \frac{3}{\sqrt{3^2-(x+2)^2}} dx =[/m]
[m]= -5\sqrt{3^2-(x+2)^2} - 3 arcsin \frac{x+2}{3} + C =-5\sqrt{5-4x-x^2} - 3 arcsin \frac{x+2}{3} + C [/m]