Задача 77749 Найти производную сложной функции. №4...
Условие
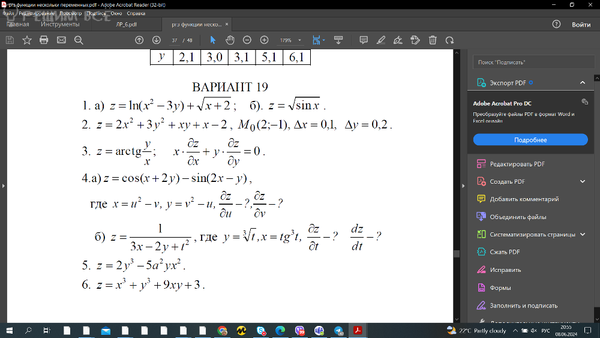
Решение
Общие формулы:
[m]\frac{dz}{du} = \frac{dz}{dx} \cdot \frac{dx}{du} + \frac{dz}{dy} \cdot \frac{dy}{du}[/m]
[m]\frac{dz}{dv} = \frac{dz}{dx} \cdot \frac{dx}{dv} + \frac{dz}{dy} \cdot \frac{dy}{dv}[/m]
Находим производные:
[m]\frac{dz}{dx} = -\sin (x + 2y) \cdot (x + 2y)'_{x} - \cos (2x - y) \cdot (2x - y)'_{x} =[/m]
[m]= -\sin (x + 2y) \cdot 1 - \cos (2x - y) \cdot 2 = -\sin (x + 2y) - 2\cos (2x - y)[/m]
[m]\frac{dz}{dy} = -\sin (x + 2y) \cdot (x + 2y)'_{y} - \cos (2x - y) \cdot (2x - y)'_{y} =[/m]
[m]= -\sin (x + 2y) \cdot 2 - \cos (2x - y) \cdot (-1) = -2\sin (x + 2y) + \cos (2x - y)[/m]
[m]\frac{dx}{du} = (u^2 - v)'_{u} = 2u; \frac{dx}{dv} = (u^2 - v)'_{v} = -1[/m]
[m]\frac{dy}{du} = (v^2 - u)'_{u} = -1; \frac{dy}{dv} = (v^2 - u)'_{v} = 2v[/m]
Подставляем в общие формулы:
[m]\frac{dz}{du} = (-\sin (x + 2y) - 2\cos (2x - y)) \cdot 2u + (-2\sin (x + 2y) + \cos (2x - y)) \cdot (-1) =[/m]
[m]= -2u \sin (x + 2y) - 4u \cos (2x - y) + 2 \sin (x + 2y) - \cos (2x - y)[/m]
[m]\frac{dz}{du} = (2 - 2u) \sin (x + 2y) - (1 + 4u) \cos (2x - y)[/m]
[m]\frac{dz}{dv} = (-\sin (x + 2y) - 2\cos (2x - y)) \cdot (-1) + (-2\sin (x + 2y) + \cos (2x - y)) \cdot 2v =[/m]
[m]= \sin (x + 2y) + 2\cos (2x - y) - 4v \sin (x + 2y) + 2v \cos (2x - y)[/m]
[m]\frac{dz}{dv} = (1 - 4v) \sin (x + 2y) + (2 + 2v) \cos (2x - y)[/m]