Задача 77746 Надо решить задачу номер 24...
Условие
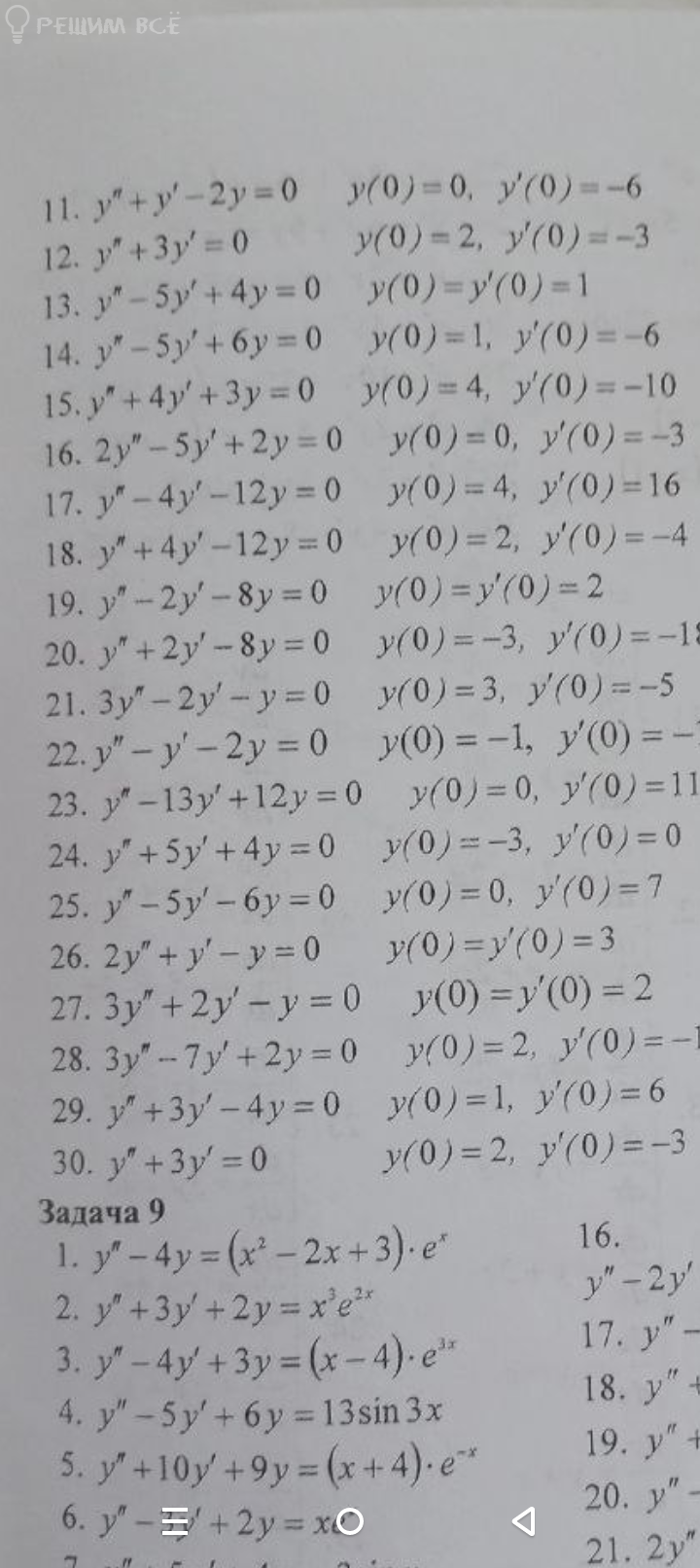
математика
174
Решение
★
Однородное линейное уравнение 2 порядка.
Характеристическое уравнение:
k^2 + 5k + 4 = 0
k1 = -1; k2 = -4
y = C1*e^(-x) + C2*e^(-4x)
Решаем задачу Коши по начальным условиям:
y' = -C1*e^(-x) - 4C2*e^(-4x)
y(0) = C1*e^(0) + C2*e^(0) = C1 + C2 = -3
y'(0) = -C1*e^(0) - 4C2*e^(0) = -C1 - 4C2 = 0
Получили систему:
{ C1 + C2 = -3
{ -C1 - 4C2 = 0
Складываем уравнения:
C1 + C2 - C1 - 4C2 = -3 + 0
-3C2 = -3
C2 = 1
C1 = -4C2 = -4
Ответ: y = e^(-x) - 4e^(-4x)