Задача 77739 Используя метод понижение порядка ,...
Условие
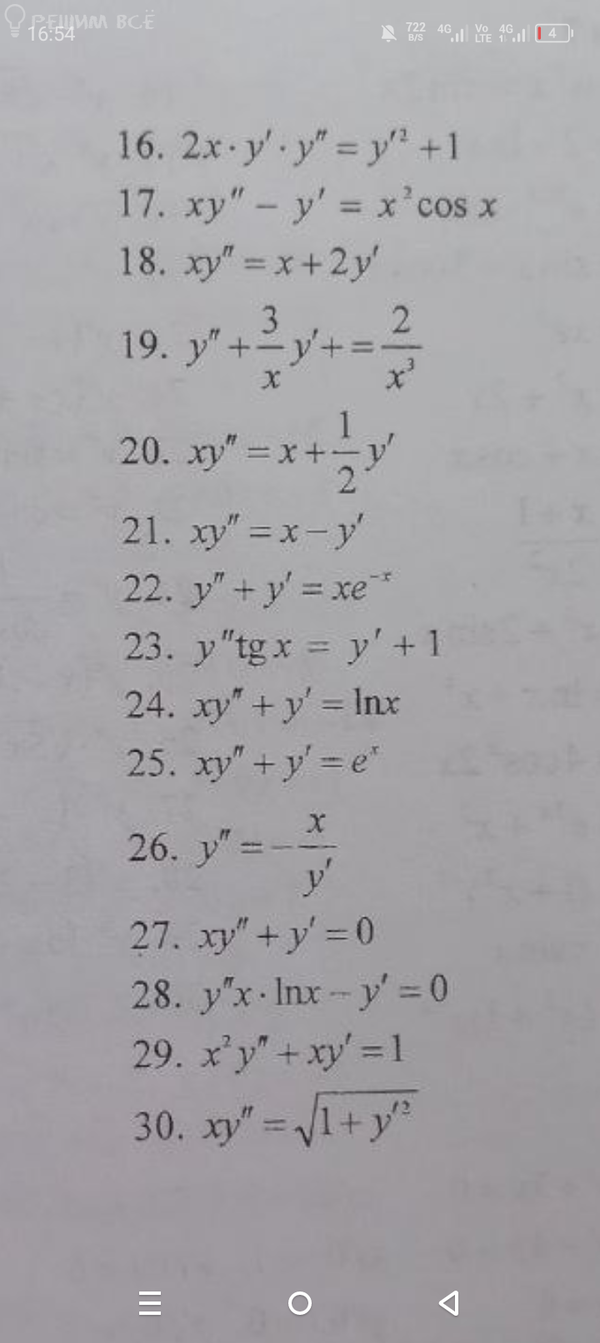
Решение
Понижение порядка. Делаем замену: y' = z; y'' = z'
[m]xz' + z = \ln x[/m]
Делим на x:
[m]z' + \frac{z}{x} = \frac{\ln x}{x}[/m]
Это неоднородное уравнение 1 порядка.
Решается заменой:
z = u*v; z' = u'*v + u*v'
[m]u'v + uv' + \frac{uv}{x} = \frac{\ln x}{x}[/m]
Выносим u за скобки:
[m]u'v + u(v' + \frac{v}{x}) = \frac{\ln x}{x}[/m]
Приравниваем скобку к 0:
[m]v' + \frac{v}{x} = 0[/m]
[m]\frac{dv}{dx} = -\frac{v}{x}[/m]
[m]\frac{dv}{v} = -\frac{dx}{x}[/m]
[m]\ln |v| = -\ln |x| = \ln |\frac{1}{x}|[/m]
[m]v = \frac{1}{x}[/m]
Подставляем в уравнение:
[m]u' \cdot \frac{1}{x} + 0 = \frac{\ln x}{x}[/m]
[m]u' = \ln x[/m]
[m]u = x \cdot \ln |x| - x + C_1[/m]
Возвращаемся к функции z = u*v:
[m]z = (x \cdot \ln |x| - x + C_1) \cdot \frac{1}{x} = \ln |x| - 1 + \frac{C_1}{x}[/m]
Возвращаемся к функции y:
[m]y' = \ln |x| - 1 + \frac{C_1}{x}[/m]
Берем интеграл:
[m]y = \int (\ln |x| - 1 + \frac{C_1}{x}) dx[/m]
[m]y = x \cdot \ln |x| - x - x + C_1 \ln |x| + C_2[/m]
[m]y = \ln |x|(x + C_1) - 2x + C_2[/m]