Задача 77736 Надо решить задачу , номер 24 Найти...
Условие
Найти общее решение 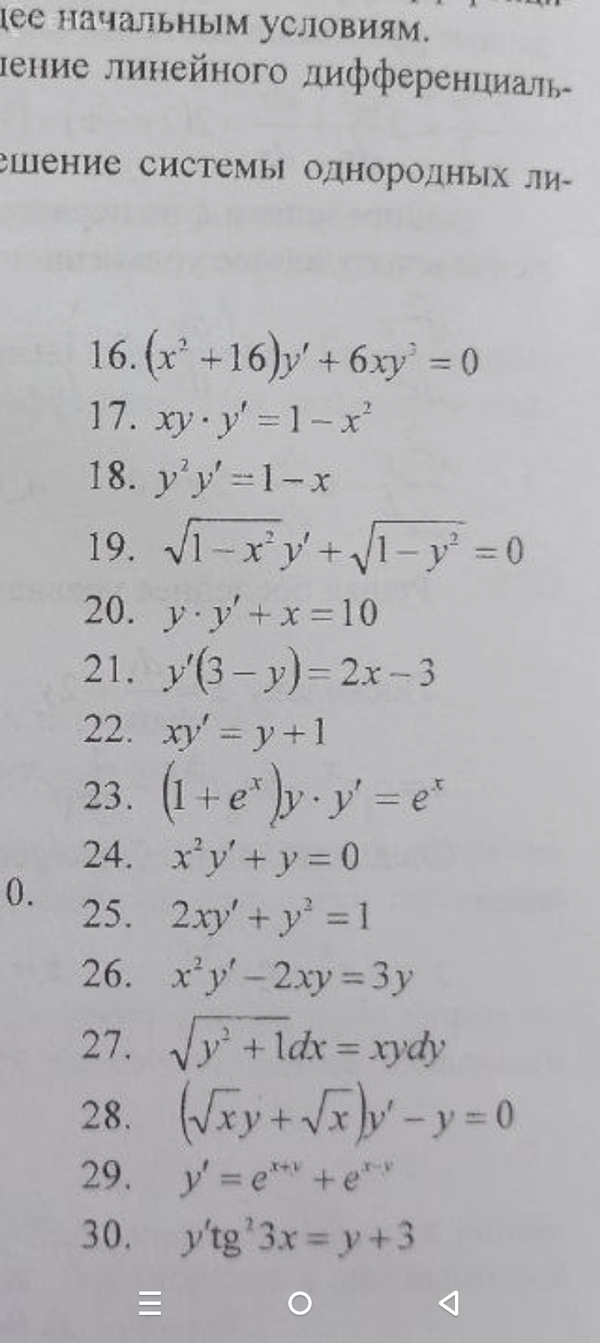
математика
154
Решение
★
Делим всё уравнение на x^2:
[m]y' + \frac{y}{x^2} = 0[/m]
Неоднородное уравнение 1 порядка.
Решается заменой:
y = u*v; y' = u'*v + u*v'
[m]u'v + uv' + \frac{uv}{x^2} = 0[/m]
Выносим u за скобки:
[m]u'v + u(v' + \frac{v}{x^2}) = 0[/m]
Скобку приравниваем к 0:
[m]v' + \frac{v}{x^2} = 0[/m]
[m]\frac{dv}{dx} = -\frac{v}{x^2}[/m]
[m]\frac{dv}{v} = -\frac{dx}{x^2}[/m]
Брем интегралы слева и справа:
[m]\ln |v| = \frac{1}{x}[/m]
[m]v = e^{1/x}[/m]
Подставляем в уравнение:
[m]u'e^{1/x} + 0 = 0[/m]
[m]u' = 0[/m]
[m]u = C[/m]
Возвращаемся к функции y = u*v:
[m]y = Ce^{1/x}[/m]