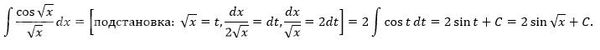Задача 77708 Нужно решить 8 и 10 примеры...

Дэнчик

5 июня 2024 г. в 11:23

Нужно решить 8 и 10 примеры

Удачник66

5 июня 2024 г. в 03:01

★

8) [m]\int \frac{\cos \sqrt{x}}{\sqrt{x}} dx[/m]
Решается заменой y = √x; dy = dx/(2√x); dx/√x = 2 dy
[m]\int \frac{\cos \sqrt{x}}{\sqrt{x}} dx = \int \cos y\ 2dy = 2\int \cos y\ dy = 2\sin y + C= 2 \sin \sqrt{x} + C[/m]

10) [m]\int \frac{x^3+1}{x^2-x}[/m]
Сначала выделяем целую часть:
[m]\int \frac{x^3+1}{x^2-x} dx =\int \frac{x^3-x^2+x^2-x+x+1}{x^2-x} dx = \int \frac{x(x^2-x)+(x^2-x)+x+1}{x^2-x} dx =[/m]
[m]= \int (x+1+\frac{x+1}{x^2-x}) dx= \int (x+1+\frac{x+1}{x(x-1)}) dx [/m]
Дальше решаем методом неопределенных коэффициентов:
[m]\frac{x+1}{x(x-1)} = \frac{A_1}{x} + \frac{A_2}{x-1} = \frac{A_1(x-1) + A_2x}{x(x-1)} = \frac{(A_1 + A_2)x - A_1}{x(x-1)}[/m]
Составляем систему по степеням:
{ A₁ + A₂ = 1
{ –A₁ = 1
Получаем:
{ A₁ = –1
{ A₂ = 2
Подставляем в наш интеграл:
[m]\int (x+1+\frac{x+1}{x(x-1)}) dx = \int (x+1-\frac{1}{x} + \frac{2}{x-1}) dx= [/m]
[m] = \frac{x^2}{2} + x - \ln|x| + 2\ln|x-1| + C = \frac{x^2}{2} + x + \ln |\frac{(x-1)^2}{x}| + C[/m]