Задача 77693 очень надо!!!!! Исследовать сходимость...
Условие
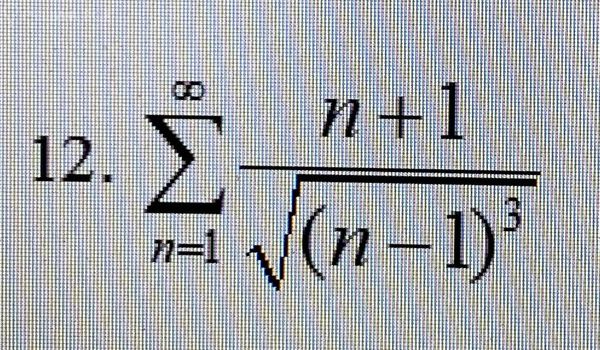
Решение
Рассмотрим ряд
[m]\Sigma \frac{n+1}{\sqrt{(n)^3}} [/m] [b](2)[/b]
Его можно преобразовать в сумму рядов:
[m]\Sigma \frac{n+1}{\sqrt{(n)^3}} = \Sigma \frac{n+1}{n^{3/2}} = \Sigma \frac{n}{n^{3/2}}+\Sigma \frac{1}{n^{3/2}} = \Sigma \frac{1}{n^{1/2}}+\Sigma \frac{1}{n^{3/2}}[/m]
Как видим, он равен сумме двух обобщенных гармонических рядов.
У первого ряда показатель k = 1/2 < 1, поэтому он расходится.
У второго ряда показатель k = 3/2 > 1, поэтому он сходится.
Сумма сходящегося и расходящегося рядов - расходится. Значит, ряд [b](2)[/b] расходится.
Заметим, что каждый член исходного ряда [b](1)[/b] больше, чем член ряда [b](2)[/b]:
[m]\frac{n+1}{\sqrt{(n-1)^3}} > \frac{n+1}{\sqrt{(n)^3}}[/m]
Так как знаменатель ряда [b](1)[/b] меньше, чем знаменатель ряда [b](2)[/b].
Признак сравнения:
Если каждый член одного ряда меньше, чем член другого ряда и этот другой ряд сходится,
то и первый ряд тоже сходится.
Если каждый член одного ряда больше, чем член другого ряда и этот другой ряд расходится, то и первый ряд тоже расходится.
Так как ряд [b](2)[/b] расходится и каждый член ряда [b](1)[/b] больше, чем ряда [b](2)[/b], то:
Ответ: ряд [b](1)[/b] расходится.