Задача 77675 Решите то что сможете , буду очень...
Условие

Решение
[m]= \frac{2}{3} \cdot 2^{3/2} + \frac{3}{4} \cdot 1^{4/3} - (\frac{2}{3} \cdot 0^{3/2} + \frac{3}{4} \cdot 0^{4/3}) = \frac{2}{3} \cdot \sqrt{8} + \frac{3}{4} = \frac{4\sqrt{2}}{3} + \frac{3}{4}[/m]
б) [m]\int_0^{\pi/2} \sin^3 x dx = \int_0^{\pi/2} \sin^2 x \cdot \sin x dx = \int_0^{\pi/2} (1-\cos^2 x) \cdot \sin x dx [/m]
Замена y = cos x; dy = -sin x dx; sin x dx = -dy; y(π/2) = cos π/2 = 0; y(0) = cos 0 = 1
[m]\int \limits_1^0 (1 - y^2)(-dy) = \int \limits_0^1 (1 - y^2) dy = (y - \frac{y^3}{3})\ |_0^1 = 1 - \frac{1}{3} - (0 - \frac{0}{3}) = \frac{2}{3}[/m]
в) [m]\int \limits_4^5 \ln (x-3) dx[/m]
Решаем методом по частям.
u = ln (x-3); dv = dx; du = 1/(x-3) dx; v = x
[m]\int \limits_4^5 \ln (x-3) dx = x \ln(x-3)\ |_4^5 - \int \limits_4^5 \frac{x}{x-3}dx =5\ln 2 - 4 \ln 1 - \int \limits_4^5 \frac{x-3+3}{x-3}dx = [/m]
[m]= 5\ln 2 - 0 - \int \limits_4^5 (1+\frac{3}{x-3})dx = 5\ln 2 - (x + 3\ln (x-3))\ |_4^5 =[/m]
[m]= 5\ln 2 - (5 + 3\ln 2 - (4 + 3\ln 1)) = 5\ln 2 - 5 - 3\ln 2 + 4 + 0) = 2\ln 2 - 1 [/m]
2) а) y = ln x; y = 0; 1 ≤ x ≤ 3
[m]S=\int_1^3 \ln x dx = x \cdot \ln x - x\ |_1^3 = 3 \ln 3 - 3 - (1 \ln 1 - 1) = 3 \ln 3 - 2[/m]
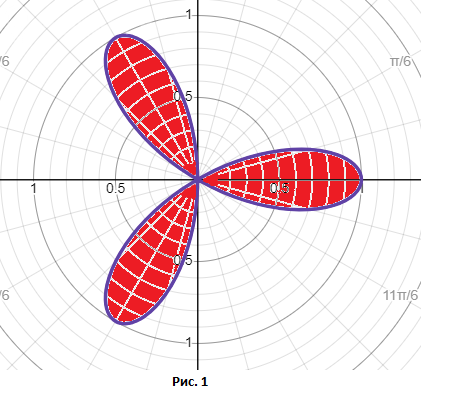
б) Не знаю, как это решать. Могу только дать рисунок. Смотрите Рисунок 1.
3) x^2 - y^2 = 16; x = 8
Объём тела вращения можно вычислить по такой формуле:
[m]V=\pi \int_{a}^b y^2(x) dx[/m]
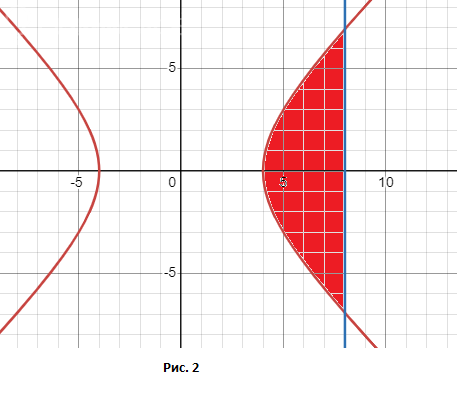
Фигура изображена на Рисунке 2. Это гипербола.
Нас интересует только правая ветвь этой гиперболы.
Вершина гиперболы: y = 0; x^2 = 16; x = 4
Границы интегрирования: a = 4; b = 8
Функция: y^2(x) = x^2 - 16
[m]V=\pi \int_{4}^8 (x^2 - 16) dx = \pi(\frac{x^3}{3} - 16x)\ |_{4}^8 = \pi(\frac{8^3}{3} - 16 \cdot 8) - (\frac{4^3}{3} - 16 \cdot 4) = [/m]
[m]= \pi(\frac{512}{3} - 128 - \frac{64}{3} + 64) = \pi(\frac{448}{3} - 64) = \frac{448 - 192}{3} \cdot \pi = \frac{256}{3} \cdot \pi[/m]
4) и 5) я не знаю, как решать.
6) а) [m]\int \limits_{-\infty}^{+\infty} \frac{dx}{x^2+4x+9} = \int \limits_{-\infty}^{+\infty} \frac{dx}{x^2+4x+4+5} = \int \limits_{-\infty}^{+\infty} \frac{dx}{(x+2)^2+5} =\frac{1}{\sqrt{5}} arctg \frac{x+2}{\sqrt{5}}\ |_{-\infty}^{+\infty}[/m]
Известно, что tg (π/2) = +oo; tg (-π/2) = -oo, поэтому считается, что:
arctg (-oo) = -π/2; arctg (+oo) = π/2. Отсюда получаем:
[m]\frac{1}{\sqrt{5}} arctg \frac{x+2}{\sqrt{5}}\ |_{-\infty}^{+\infty} = \frac{1}{\sqrt{5}} \cdot \frac{\pi}{2} - (\frac{1}{\sqrt{5}} \cdot (-\frac{\pi}{2})) = \frac{\pi}{2\sqrt{5}} + \frac{\pi}{2\sqrt{5}} = \frac{\pi}{\sqrt{5}} [/m]
б) [m]\int \limits_0^2 \frac{dx}{(x-2)^2} = -\frac{1}{x-2}\ |_0^2 = -\frac{1}{2-2} + \frac{1}{0-2} = \infty[/m]
Интеграл расходится.