Задача 77674 Вычислить площади фигур, ограниченных...
Условие
ными линиями. Выполнить чертеж.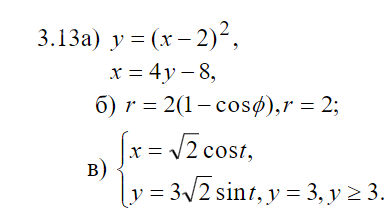
Решение
Выразим y через x во второй функции:
y = (x + 8)/4
Находим пределы интегрирования, для этого приравниваем правые части:
(x - 2)^2 = (x + 8)/4
x^2 - 4x + 4 - (x + 8)/4 = 0
4x^2 - 16x + 16 - x - 8 = 0
4x^2 - 17x + 8 = 0
D = (-17)^2 - 4*4*8 = 289 - 128 = 161
x1 = (17 - sqrt(161))/8; x2 = (17 + sqrt(161))/8
Очень "кривые" границы получились, посчитать площадь трудно.
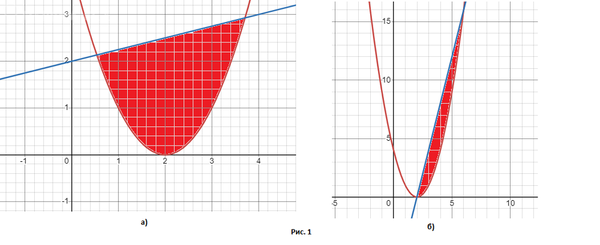
Чертеж смотрите на Рис. 1 а). Площадь закрашена красным.
Площадь находим как разность интегралов:
[m]S=\int \limits_{(17 - \sqrt{161})/8}^{(17 + \sqrt{161})/8} (\frac{x+8}{4} - (x - 2)^2)dx = \int \limits_{(17 - \sqrt{161})/8}^{(17 + \sqrt{161})/8} (\frac{x}{4}+2 - (x - 2)^2)dx =[/m]
[m]= (\frac{x^2}{8} + 2x - \frac{(x-2)^3}{3})\ |_{(17 - \sqrt{161})/8}^{(17 + \sqrt{161})/8} = [/m]
[m]=\frac{((17 + \sqrt{161})/8)^2}{8} + 2 \cdot \frac{17 + \sqrt{161}}{8} - \frac{1}{3}((17 + \sqrt{161})/8-2)^3 -[/m]
[m] -(\frac{((17 - \sqrt{161})/8)^2}{8} + 2 \cdot \frac{17 - \sqrt{161}}{8} - \frac{1}{3}((17 - \sqrt{161})/8-2)^3)[/m]
Дальше считайте сами. Немного облегчу подсчеты:
x1 - 2 = (17 - sqrt(161))/8 - 2 = (1 - sqrt(161))/8
x2 - 2 = (17 + sqrt(161))/8 - 2 = (1 + sqrt(161))/8
Но я подозреваю, что в уравнении прямой опечатка, должно быть:
y = 4x - 8
Тогда было бы намного проще:
(x - 2)^2 = 4x - 8
x^2 - 4x + 4 - 4x + 8 = 0
x^2 - 8x + 12 = 0
x1 = 2; x2 = 6
Чертеж смотрите на Рис. 1 б). Площадь закрашена красным.
[m]S = \int \limits_2^6 (4x - 8 - (x - 2)^2)dx = 2x^2 - 8x - \frac{(x-2)^3}{3}\ |_2^6 = 2 \cdot 6^2 - 8 \cdot 6 - \frac{4^3}{3} - (2 \cdot 2^2 - 8 \cdot 2 - \frac{0^3}{3}) =[/m]
[m]= 72 - 48 - \frac{64}{3} - 8 + 16 + 0 = 42 - \frac{64}{3} = 42 - 21\frac{1}{3} = 20\frac{2}{3} [/m]
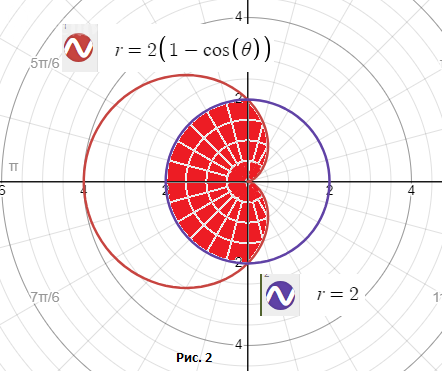
б) Функция в полярных координатах.
r = 2(1 - cos φ ); r = 2
Я не знаю, как считать площадь в этом случае.
Могу только дать чертеж. Смотрите на Рис. 2. Площадь закрашена красным.
в) Функция в параметрическом виде.
{ x = sqrt(2)*cos t
{ y = 3sqrt(2)*sin t
{ y = 3; y ≥ 3
Переводим функцию из параметрического вида в обычный.
{ x^2 = 2cos^2 t
{ y^2 = 9*2*sin^2 t
{ y = 3; y ≥ 3
Выразим sin t и cos t:
{ cos^2 t = x^2/2
{ sin^2 t = y^2/18
{ y = 3; y ≥ 3
Как известно, sin^2 t + cos^2 t = 1. Складываем 1 и 2 уравнения:
{ x^2/2 + y^2/18 = 1
{ y = 3; y ≥ 3
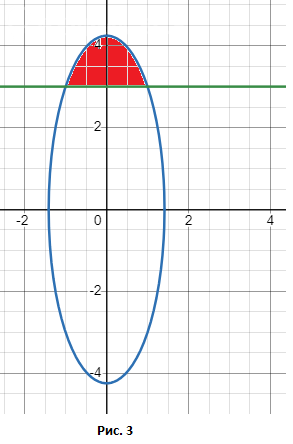
Чертеж смотрите на Рис. 3. Площадь закрашена красным.
Умножаем 1 уравнение на 18:
{ 9x^2 + y^2 = 18
{ y = 3; y ≥ 3
Выражаем y через x в 1 уравнении:
{ y^2 = 18 - 9x^2 = 9(2 - x^2)
{ y = 3; y ≥ 3
Получаем:
{ y = 3sqrt(2 - x^2)
{ y = 3; y ≥ 3
Находим пределы интегрирования, для этого приравниваем правые части:
3sqrt(2 - x^2) = 3
sqrt(2 - x^2) = 1
2 - x^2 = 1
x^2 = 1
x1 = -1; x2 = 1
Площадь находим как разность интегралов:
[m]S= \int \limits_{-1}^1 (3\sqrt{2 - x^2} - 3)dx = 3\int \limits_{-1}^1 (\sqrt{2 - x^2} - 1)dx = 3(\frac{x}{2} \cdot \sqrt{2 - x^2} + \frac{2}{2}\cdot \arcsin \frac{x}{\sqrt{2}})\ |_{-1}^1 =[/m]
[m]= 3(\frac{1}{2} \cdot \sqrt{2 - 1^2} + \arcsin \frac{1}{\sqrt{2}}) - 3(\frac{-1}{2} \cdot \sqrt{2 - (-1)^2} + \arcsin \frac{-1}{\sqrt{2}}) = [/m]
[m]= 3(\frac{1}{2} + \frac{\pi}{4}) - 3(-\frac{1}{2} - \frac{\pi}{4}) = \frac{3}{2} + \frac{3\pi}{4} + \frac{3}{2} + \frac{3\pi}{4} = 3 + \frac{3\pi}{2}[/m]