Задача 77652 При каких значениях а уравнение...

66558df13528112db82d8dbd

5/28/2024 7:57:38 AM

При каких значениях а уравнение |2|x|-3|=a-3 имеет один корень

626fab9a354ab65fb2f43abb

5/28/2024 4:32:10 PM

★

|2|x| - 3| = a - 3

1) x < 0, тогда |x| = -x
|-2x - 3| = a - 3
1а) -2x - 3 < 0
2x > -3
x > -3/2
Получаем: x ∈ (-3/2; 0)
Тогда |-2x - 3| = 2x + 3
2x + 3 = a - 3
2x = a - 6
x = a/2 - 3
Если x = -3/2, то a/2 = -3/2 + 3 = 3/2; отсюда a = 3
Если x = 0, то a/2 - 3 = 0; отсюда a = 6
Значит, при a ∈ (3; 6) будет x = a/2 - 3

1б) -2x - 3 ≥ 0
2x ≤ -3
x ≤ -3/2
Получаем: x ∈ (-oo; -3/2]
Тогда |-2x - 3| = -2x - 3
-2x - 3 = a - 3
-2x = a
x = -a/2
Если x = -3/2, то -3/2 = -a/2; отсюда a = 3
Так как а и x имеют разные знаки, и x ≤ -3/2, то a ≥ 3.
Значит, при a ∈ [3; +oo) будет x = -a/2

2) x ≥ 0, тогда |x| = x
|2x - 3| = a - 3
2а) 2x - 3 < 0
2x < 3
x < 3/2
Получаем: x ∈ [0; 3/2)
Тогда |2x - 3| = -2x + 3
-2x + 3 = a - 3
-2x = a - 6
x = -a/2 + 3
Если x = 0, то -a/2 + 3 = 0; отсюда a = 6
Если x = 3/2, то -a/2 = 3/2 - 3 = -3/2; отсюда a = 3
Значит, при a ∈ (3; 6] будет x = -a/2 + 3

2б) 2x - 3 ≥ 0
x ≥ 3/2
Получаем: x ∈ [3/2; +oo)
Тогда |2x - 3| = 2x - 3
2x - 3 = a - 3
2x = a
x = a/2
Если x = 3/2, то 3/2 = a/2, отсюда a = 3
Так как а и x имеют одинаковые знаки и x ≥ 3/2, то a ≥ 3
Значит, при a ∈ [3; +oo) будет x = a/2

Вывод:
1) При a ∈ (-oo; 3) корней нет.
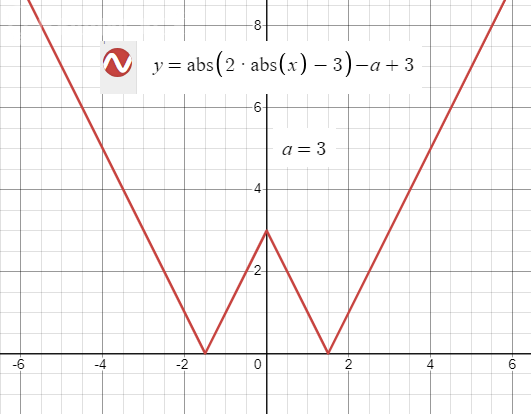
2) При a = 3 корней два: x1 = -a/2 = -3/2; x2 = a/2 = 3/2
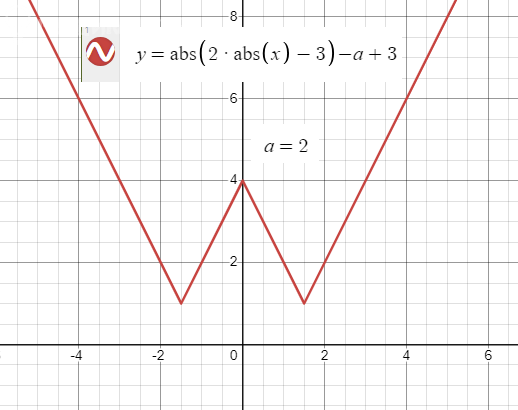
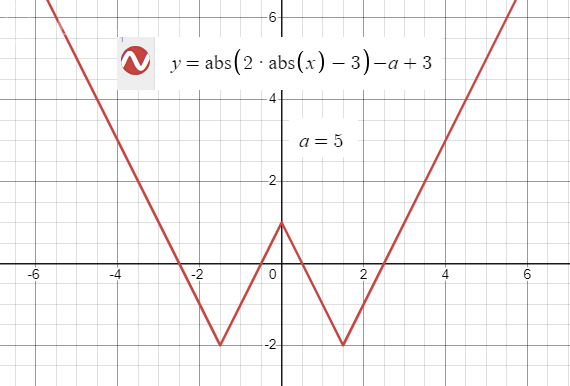
3) При a ∈ (3; 6) будет 4 корня: x1 = a/2 - 3; x2 = -a/2; x3 = -a/2 + 3; x4 = a/2
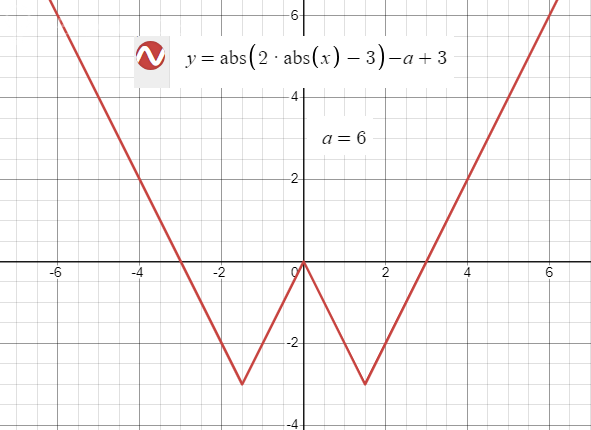
4) При a = 6 будет 3 корня: x1 = -a/2 = -3; x2 = -a/2 + 3 = 0; x3 = a/2 = 3
5) При a ∈ (6; +oo) будет 2 корня: x1 = -a/2; x2 = a/2

Ответ: Ни при каком значении а не бывает 1 корня.
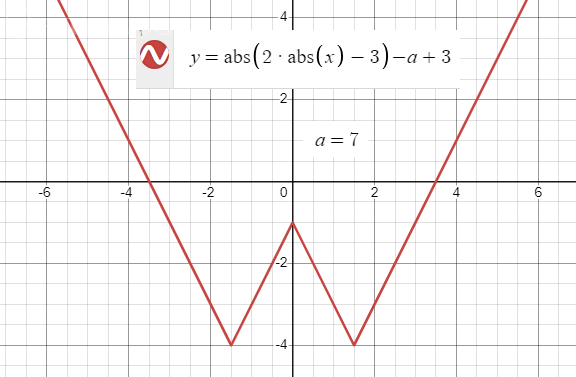
Графики показаны на рисунках. Номера рисунков соответствуют пунктам в Выводе.