Задача 77646 ...

66538da93528112db82d8c0f

5/26/2024 7:31:50 PM

В основі прямої призми лежить рівнобедрений трикутник з
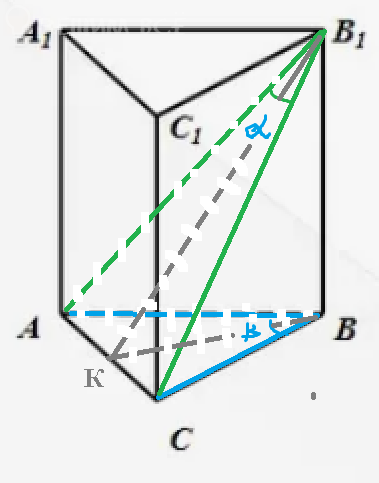
кутом β при вершині. Через дві рівні діагоналі двох бічних
граней, кут між якими дорівнює α, проведено переріз,
площа якого дорівнює S. Знайдіть об'єм циліндра,
описаного навколо даної призми. з малюнком

5f3ea7e3faf909182968ddd9

5/26/2024 8:00:12 PM

★

S_(сечения)=(1/2) АВ_(1)*В_(1)C*sin ∠ AB_(1)C

AB_(1)=B_(1)C ( равные проекции АВ=ВС имеют равные наклонные)
S=(1/2)AB^2_(1)*sin α

AB^2_(1)=2S/sin α

AB_(1)=sqrt(2S/sin α )

Δ АВС - равнобедренный

ВК ⊥ АС

ВК - высота и медиана

АК=КС

Δ AB_(1)C- равнобедренный . так как AB_(1)=B_(1)C ( равные проекции АВ=ВС имеют равные наклонные)

В_(1)K - медиана, а значит и высота


АК=AB_(1)*sin∠ AB_(1)C

AC=2*AB_(1)*sin( α /2)=2*sqrt(2S/sin α )*sin( α /2)

АВ=АК/sin( β /2)=sqrt(2S/sin α )*sin( α /2)


ВВ^2_(1)=AB^2_(1)-AB^2

BB_(1)=H

R=АВ*ВС*АС./4S_( Δ АВС)


V_(цилиндра)=π*R^2*H


Можно ввести переменную

Пусть АС=х
Тогда из Δ АВК

sin( β /2)=AK/AB

АВ=AK/sin (β /2)=x/(2sin( β /2))

Из Δ АВ_(1)К

AB_(1)=AK/sin( α /2)=x/(2sin( α /2))

S_(сечения)=(1/2) АВ_(1)*В_(1)C*sin ∠ AB_(1)C=(1/2)*(x/(2sin( α /2)))*(x/(2sin( α /2)))*sin α

S=(x^2/4)ctg( α /2)

x=2sqrt(S/ctg( α /2))

BB^2_(1)=(x/(2sin( α /2)))^2-(x/(2sin( β /2)))^2

BB_(1)=H_(призмы)=Н_(цилиндра)