Задача 77607 В ящике 100 шаров, из них 20 синих, 30...
Условие
фиксируют его цвет и возвращают его в ящик. Проводится 6 таких испытаний.
X – число вынутых черных шаров в этих испытаниях. Составьте закон распределения дискрет-
ной случайной величины
X
, вычислите ее математическое ожидание, дисперсию, среднее квадратическое отклонение, а также начертите график функции распределения.
Решение
может принимать значения:
0;1;2;3;4;5;6
Вероятность извлечь черный шар в одном испытании
p=30/100=0,3
q=1-p=1-0,3=0,7 -вероятность извлечь в одном испытании шар (но не черный)
Решаем семь задач
Х=0
Находим вероятность, соответствующую этому событию
Применяем формулу Бернулли
Это повторные испытания с двумя исходами
Вынули 6 шаров, черных там нет
Х=0
p_(0)=(0,7)^6=0,117649 ≈ 0,12
Х=1
Находим вероятность, соответствующую этому событию
Вынули 6 шаров, черный шар встретился один раз
p_(1)=C^(1)_(6)0,3*0,7^5=0,302526 ≈ 0,3
X=2
p_(2)=C^(2)_(6)0,3^2*0,7^4=0,324135≈ 0,32
И так далее...
X=6
p_(6)=0,3^6=0,000729≈ 0,0007
Закон - таблица...
В первой строке значения случайной величины, во второй - соответствующие вероятности...
По определению математическое ожидание
M(X)=0·p_(0)+1·p_(1)+2·p_(2)+3·p_(3)+4·p_(4)+5·p_(5)+6·p_(6)
Дисперсию вычисляем по формуле:
D(X)=M(X^2)–(M(X))^2
M(X^2)=0^2·p_(0)+1^2·p_(1)+2^2·p_(2)+3^2·p_(3)+4^2·p_(4)+5^2·p_(5)+6^2·p_(6)
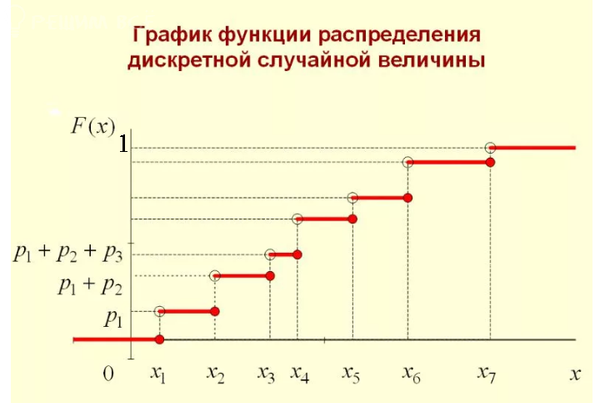
Функция распределения:
[m]F(x)=\left\{\begin {matrix}0; если x ≤ 0\\p_{0} ;если 0 <x ≤1\\p_{0}+p_{1}; если 1<x ≤ 2\\p_{0}+p_{1}+p_{2};если 2<x ≤ 3\\p_{0}+p_{1}+p_{2}+p_{3};если 3<x ≤ 4\\p_{0}+p_{1}+p_{2}+p_{3}+p_{4};если 4<x ≤5\\p_{0}+p_{1}+p_{2}+p_{3}+p_{4}+p_{5};если 5<x ≤6\\1; если x >6\end {matrix}\right.[/m]
Функция распределения:
[m]F(x)=\left\{\begin {matrix}0; если x ≤ 0\\0,12 ;если 0 <x ≤1\\0,12+0,3=0,42; если 1<x ≤ 2\\0,12+0,3+0,32=0,74;если 2<x ≤ 3\\0,74+p_{3};если 3<x ≤ 4\\0,74+p_{3}+p_{4};если 4<x ≤5\\0,74+p_{3}+p_{4}+p_{5};если 5<x ≤6\\1; если x >6\end {matrix}\right.[/m]
График функции распределения - ступенчатая функция вида: