Задача 77589 ...
Условие
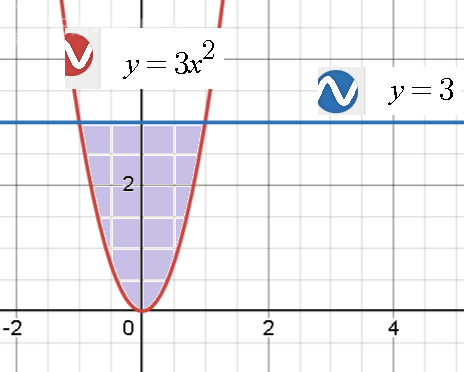
D ∫ ∫(x+1)y^2dxdy, D: y=3x^2 y=3, заранее спасибо!
математика ВУЗ
137
Решение
★
-1 ≤ x ≤ 1
0 ≤ y ≤ 3
∫∫_(D)(x+1)y^2dxdy= ∫^(1) _(-1) ( [red]∫^(3) _(0)(x+1)*y^2dy[/red])dx=
= ∫^(1) _(-1) (x+1)*( [red]∫^(3) _(0)y^2dy[/red])dx=
=∫^(1) _(-1) (x+1)*( [red](y^3/3)|^(3) _(0))[/red])dx=
=∫^(1) _(-1) (x+1)*( [red](3^3/3)-(0^3/3))[/red])dx=
=∫^(1) _(-1) (x+1)*( [red]9[/red])dx=
[red]=9[/red]∫^(1) _(-1) (x+1)dx=
[red]=9[/red]((x+1)^2/2)|^(1) _(-1) [red]=9[/red]*(((1+1)^2/2)-0)=[b]18[/b]