Задача 77575 Исследование кривых второго порядка:...
Условие

Решение


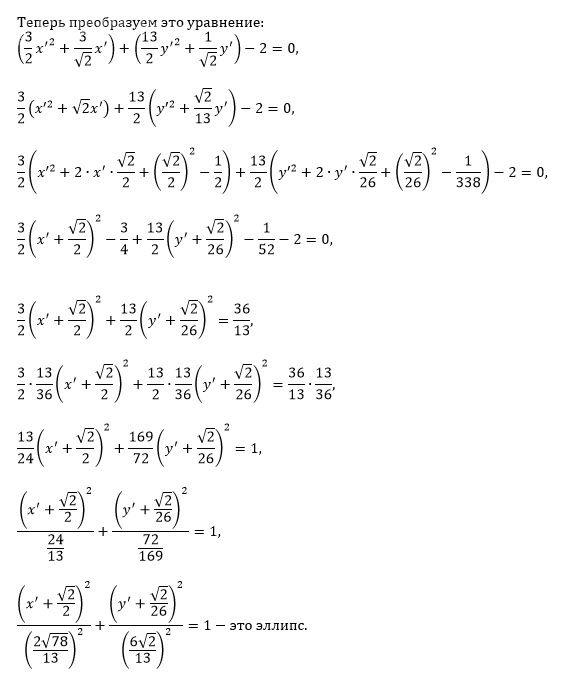

Все решения
Здесь нужно избавиться от члена 5xy. Для этого нужно повернуть оси на угол α.
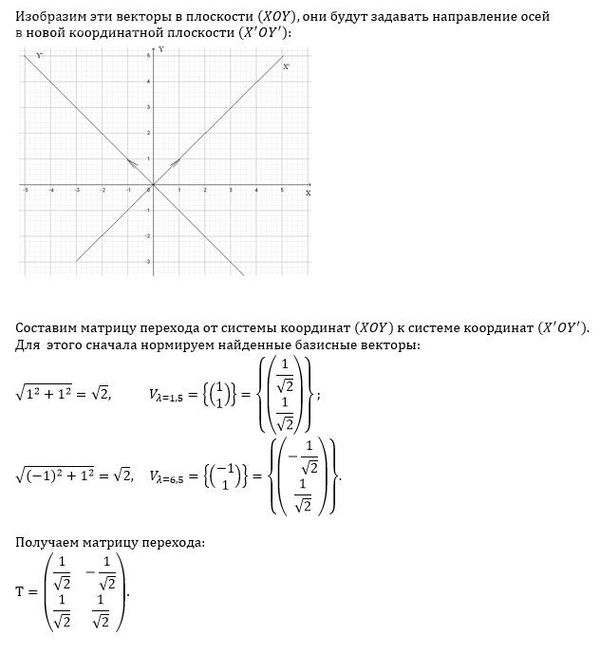
Для поворота применяем такую замену:
{ x = X*cos α - Y*sin α
{ y = X*sin α + Y*cos α
Подставляем:
4(X*cos α - Y*sin α)^2 - 5(X*cos α - Y*sin α)(X*sin α + Y*cos α) + 4(X*sin α + Y*cos α)^2 +
+ (X*cos α - Y*sin α) + 2(X*sin α + Y*cos α) - 2 = 0
Возводим в квадраты и умножаем:
4(X^2*cos^2 α - 2XY*sin α*cos α + Y^2*sin^2 α) -
- 5(X^2*sin α*cos α - XY*sin^2 α + XY*cos^2 α - Y^2*sin α*cos α) +
+ 4(X^2*sin^2 α + 2XY*sin α*cos α + Y^2*cos^2 α) +
+ X*cos α - Y*sin α + 2X*sin α + 2Y*cos α - 2 = 0
Раскрываем скобки. Собираем отдельно X и Y:
X^2*(4cos^2 α - 5sin α*cos α + 4sin^2 α) + Y^2*(4sin^2 α + 5sin α*cos α + 4cos^2 α) +
+ XY*(-8sin α*cos α + 5sin^2 α - 5cos^2 α + 8sin α*cos α) +
+ X(2sin α + cos α) + Y(-sin α + 2cos α) - 2 = 0
Скобку при XY приравниваем к 0, находим угол α.
-8sin α*cos α + 5sin^2 α - 5cos^2 α + 8sin α*cos α = 0
5sin^2 α - 5cos^2 α = 0
sin^2 α - cos^2 α = 0
sin^2 α = cos^2 α
tg^2 α = 1
Берем положительное решение:
tg α = 1
α = π/4
[b]sin α = sin π/4 = sqrt(2)/2[/b]
[b]cos α = cos π/4 = sqrt(2)/2[/b]
[b]sin^2 α= 1/2; cos^2 α = 1/2; sin α*cos α = 1/2[/b]
Подставляем в наше уравнение:
X^2*(4*1/2 - 5*1/2 + 4*1/2) + Y^2*(4*1/2 + 5*1/2 + 4*1/2) + XY*0 +
+ X(2*sqrt(2)/2 + sqrt(2)/2) + Y(-sqrt(2)/2 + 2*sqrt(2)/2) - 2 = 0
Приводим подобные:
X^2*3/2 + Y^2*13/2 + X*3sqrt(2)/2 + Y*sqrt(2)/2 - 2 = 0
Получили обычное уравнение без XY, выделяем полные квадраты:
3/2*(X^2 + 2*sqrt(2)/2*X + (sqrt(2)/2)^2 - (sqrt(2)/2)^2) +
+ 13/2(Y^2 + 2*sqrt(2)/26*Y + (sqrt(2)/26)^2 - (sqrt(2)/26)^2) = 2
Сворачиваем полные квадраты:
3/2*(X + sqrt(2)/2)^2 - 3/2*1/2 + 13/2*(Y + sqrt(2)/26)^2 - 13/2*2/26^2 = 2
3/2*(X + sqrt(2)/2)^2 + 13/2*(Y + sqrt(2)/26)^2 = 2 + 3/4 + 1/52
3/2*(X + sqrt(2)/2)^2 + 13/2*(Y + sqrt(2)/26)^2 = 104/52 + 39/52 + 1/52
3*(X + sqrt(2)/2)^2 + 13*(Y + sqrt(2)/26)^2 = 144/52
3*(X + sqrt(2)/2)^2 + 13*(Y + sqrt(2)/26)^2 = 36/13
Умножаем всё уравнение на 13/36, чтобы справа была 1:
39/36*(X + sqrt(2)/2)^2 + 169/36*(Y + sqrt(2)/26)^2 = 1
(X + sqrt(2)/2)^2 / (36/39) + (Y + sqrt(2)/26)^2 / (36/169) = 1
(X + sqrt(2)/2)^2 / (6/sqrt(39))^2 + (Y + sqrt(2)/26)^2 / (6/13)^2 = 1
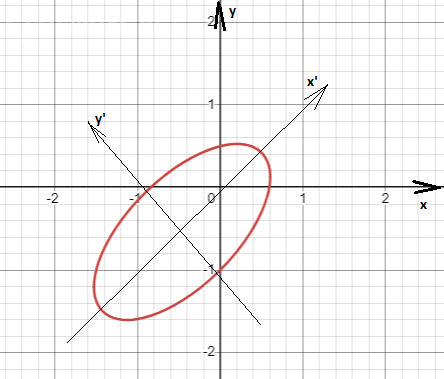
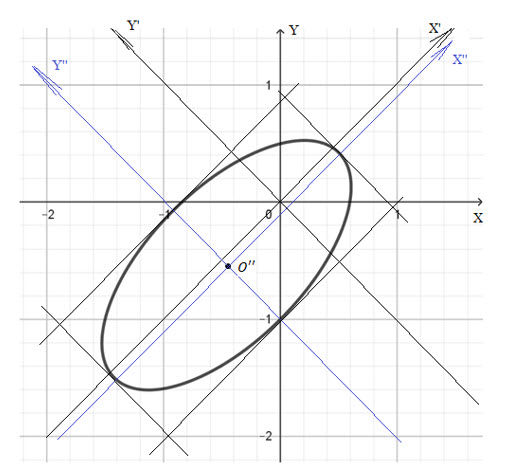
Это эллипс, повернутый на π/4 радиан, с центром A(-sqrt(2)/2; -sqrt(2)/26)
и полуосями a = 6/sqrt(39); b = 6/13
Рисунок прилагается.